
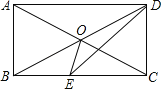
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
【答案】(1)详见解析;(2)1
【解析】
(1)证出∠BAD=∠BCD,得出四边形ABCD是平行四边形,得出OA=OC,OB=OD,证出AC=BD,即可解决问题;
(2)作OF⊥BC于F.求出EC、OF即可解决问题;
(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形.
(2)解:作OF⊥BC于F,如图所示.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=![]() CD=1,
CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积=![]() ECOF=1.
ECOF=1.


科目:初中数学 来源: 题型:
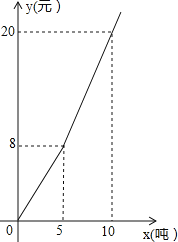
【题目】浙江实施“五水共治“以来,越来越重视节约用水,某地对居民用水按阶梯水价方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元),请根据图象信息,回答下列问题.
(1)请写出y与x的函数关系式;
(2)若某个家庭有5人,响应节水号召,计划控制1月份的生活用水费不超过76元,则该家庭这个月最多可以用多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,已知格点△ABC和格点O.
(1)画出△ABC关于点O对称的△A′B′C′;
(2)若以点A、O、C、D为顶点的四边形是平行四边形,则点D的坐标为__.(写出所有可能的结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强中学生的体质,某校食堂每天都为学生提供一定数量的水果,学校李老师为了了解学生喜欢吃哪种水果,进行了抽样调查,调查分为五种类型:A喜欢吃苹果的学生;B喜欢吃桔子的学生;C.喜欢吃梨的学生;D.喜欢吃香蕉的学生;E喜欢吃西瓜的学生,并将调查结果绘制成图1和图2 的统计图(不完整).请根据图中提供的数据解答下列问题:

(1)求此次抽查的学生人数;
(2)将图2补充完整,并求图1中的![]() ;
;
(3)现有5名学生,其中A类型2名,B类型2名,从中任选2名学生参加很体能测试,求这两名学生为同一类型的概率(用列表法或树状图法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+2x+k+1与x轴交与A、B两点,与y轴交与点C(0,-3).
(1)求抛物线的对称轴及k的值;
(2)求抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标.
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2![]() ,求正方形ADCE周长.
,求正方形ADCE周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,下列结论中错误的有( )
①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经销店为厂家代销一种新型环保水泥,当每吨售价为260元时,月销售量为45吨,每售出1吨这种水泥共需支付厂家费用和其他费用共100元.该经销店为扩大销售量、提高经营利润,计划采取降价的方式进行促销,经市场调查发现,当每吨售价每下降10元时,月销售量就会增加7.5吨.
(1)当每吨售价是240元时,此时的月销售量是多少吨.
(2)该经销店计划月利润为9000元而且尽可能地扩大销售量,则售价应定为每吨多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
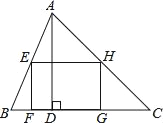
【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=![]() EH.
EH.
(1)求证:△AEH∽△ABC;
(2)求矩形EFGH的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com