
【题目】如图,矩形ABCD中,AD>AB,连接AC,将线段AC绕点A顺时针旋转90得到线段AE,平移线段AE得到线段DF(点A与点D对应,点E与点F对应),连接BF,分别交直线AD,AC于点G,M,连接EF.
(1) 依题意补全图形;
(2) 求证:EG⊥AD;
(3) 连接EC,交BF于点N,若AB=2,BC=4,设MB=a,NF=b,试比较![]() 与
与![]() 之间的大小关系,并证明.
之间的大小关系,并证明.
【答案】(1)见解析;(2)见解析;(3)![]() <
<![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据题目要求作出图形即可;
(2)连EF,EG,延长AB交EF于点H,先依据矩形与平行线的性质,等角的余角相等,旋转的性质,得到![]() ≌
≌![]() (AAS),依据全等的性质及等量代换可得
(AAS),依据全等的性质及等量代换可得![]() ,结合依据相似的判定与性质,得到
,结合依据相似的判定与性质,得到![]() ,再依据SAS可证明
,再依据SAS可证明![]() ≌
≌![]() ,依据全等的性质得到
,依据全等的性质得到![]() ,即EG⊥AD;
,即EG⊥AD;
(3)依据勾股定理求出![]() ,依据平行线分线段成比例可分别证
,依据平行线分线段成比例可分别证![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,
,![]() ∽
∽![]() ,依据相似三角形的性质得到
,依据相似三角形的性质得到![]() 、
、![]() 、
、![]() 、
、![]() ,即可求出
,即可求出![]() =
=![]() =9+5
=9+5![]() <
<![]() .
.
解:(1)补全图形如下:
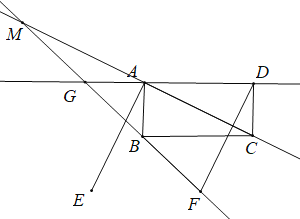
(2)连EF,EG,延长AB交EF于点H,设![]() ,
,![]() ,
,
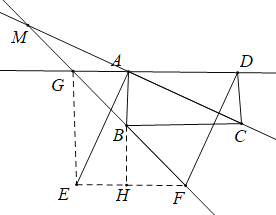
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵矩形ABCD,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ≌
≌![]() (AAS),
(AAS),
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() (SAS),
(SAS),
∴![]() ,
,
∴EG⊥AD;
(3) 当AB=2,BC=4,MB=a,NF=b时,![]() <
<![]() ,理由如下:
,理由如下:
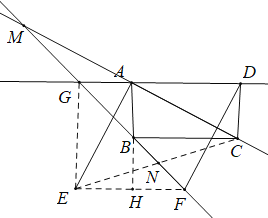
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵![]()
![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() =
=![]() =9+5
=9+5![]() <
<![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
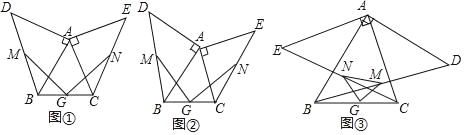
【题目】(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是__________;位置关系是__________.
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据以下信息,解答下列问题.

(1)小华同学设乙型机器人每小时搬运xkg产品,可列方程为 .
小惠同学设甲型机器人搬运800kg所用时间为y小时,可列方程为 .
(2)请你按照(1)中小华同学的解题思路,写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
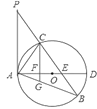
【题目】如图,已知在![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,且交
的直径,且交![]() 于点
于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)在满足(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的半径及
的半径及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:宽与长的比是![]() (约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:
(约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:![]() ).
).
第一步:在矩形纸片一端 ,利用图1的方法折出一个正方形,然后把纸片展平;
第二步:如图2,把这个正方形折成两个相等的矩形,再把纸片展平;
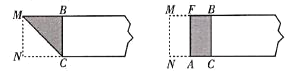
图1 图2
第三步:折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处;
处;
第四步:展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ,则图4中就会出现黄金矩形.
,则图4中就会出现黄金矩形.
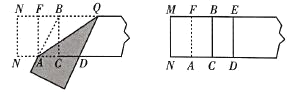
图3 图4
(1)在图3中![]() _________ (保留根号);
_________ (保留根号);
(2)如图3,则四边形![]() 的形状是_________;
的形状是_________;
(3)在图4中黄金矩形是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
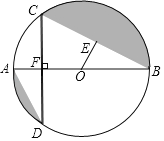
【题目】如图,AB为⊙O直径,OE⊥BC垂足为E,AB⊥CD垂足为F.
(1)求证:AD=2OE;
(2)若∠ABC=30°,⊙O的半径为2,求两阴影部分面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
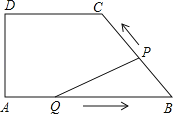
(1)当t为何值时,P,Q两点同时停止运动;
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com