
【题目】如图,已知在![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,且交
的直径,且交![]() 于点
于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)在满足(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的半径及
的半径及![]() 的值.
的值.
【答案】(1)见解析;(2)AC=![]() ;(3)sin∠ACE=
;(3)sin∠ACE=![]() .
.
【解析】
(1)根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案;
(2)首先得出△CAG∽△BAC,进而得出AC2=AGAB,求出AC即可;
(3)先求出AF的长,根据勾股定理得:AG=![]() ,即可得出sin∠ADB的值,利用∠ACE=∠ACB=∠ADB,求出即可.
,即可得出sin∠ADB的值,利用∠ACE=∠ACB=∠ADB,求出即可.
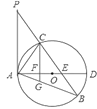
解:(1)证明:连接CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD+∠ADC=90°,
又∵∠PAC=∠PBA,∠ADC=∠PBA,
∴∠PAC=∠ADC,
∴∠CAD+∠PAC=90°,即∠PAD=90°,
∴PA⊥OA.
又∵AD是⊙O的直径,
∴PA是⊙O的切线;

(2)由(1)知,PA⊥AD,
又∵CF⊥AD,
∴CF∥PA,
∴∠GCA=∠PAC,
又∵∠PAC=∠PBA,
∴∠GCA=∠PBA,
又∵∠CAG=∠BAC,
∴△CAG∽△BAC,
∴![]() ,即AC2=AGAB,
,即AC2=AGAB,
∵AGAB=48,
∴AC2=48.
∴AC=![]() .
.
(3)设AF=x,
∵AF:FD=1:2,
∴FD=2x.
∴AD=AF+FD=3x.
在Rt△ACD中,
∵CF⊥AD,
由射影定理得:AC2=AFAD,
即3x2=48.
解得;x=4.
∴AF=4,AD=12.
∴⊙O半径为6.
在Rt△AFG中,∵AF=4,GF=2,
∴根据勾股定理得:AG=![]() ,
,
由(2)知,AGAB=48,
∴AB=![]() ,
,
连接BD,∵AD是⊙O的直径,
∴∠ABD=90°.
在Rt△ABD中,
∵sin∠ADB=![]() ,AD=12,AB=
,AD=12,AB=![]() ,
,
∴sin∠ADB=![]() .
.
∵∠ACE=∠ACB=∠ADB,
∴sin∠ACE=![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 与直线
与直线![]() 交于
交于![]() 两点,且
两点,且![]() 两点之间的抛物线上总有两个纵坐标相等的点.
两点之间的抛物线上总有两个纵坐标相等的点.
(1)求证:![]() ;
;
(2)过![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于
于![]() ,
,![]() ,且当
,且当![]() ,
,![]() ,
,![]() 三点共线时,
三点共线时,![]() 轴.
轴.
①求![]() 的值:
的值:
②对于每个给定的实数![]() ,以
,以![]() 为直径的圆与直线
为直径的圆与直线![]() 总有公共点,求
总有公共点,求![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,王老师出示一道数学题目:“在平面直角坐标系![]() 中,当
中,当![]() 为何值时,抛物线
为何值时,抛物线![]() 与直线段
与直线段![]() 有唯一公共点或有两个公共点?”某学习小组经探究得到以下四个结论:
有唯一公共点或有两个公共点?”某学习小组经探究得到以下四个结论:
①当![]() 时,有唯一公共点;
时,有唯一公共点;
②若![]() 为整数,则仅当
为整数,则仅当![]() 的值为4或5或6或7时,才有唯一公共点;
的值为4或5或6或7时,才有唯一公共点;
③若![]() 为整数,则当
为整数,则当![]() 的值为1或2或3时,有两个公共点;
的值为1或2或3时,有两个公共点;
④当![]() 时,有两个公共点.其中正确的结论有( )
时,有两个公共点.其中正确的结论有( )
A.①②④B.①②③C.①③D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 、
、![]() 均在线段
均在线段![]() 上,且
上,且![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .在
.在![]() 中,若
中,若![]() 轴,
轴,![]() 轴,则称
轴,则称![]() 为点
为点![]() 、
、![]() 的“榕树三角形”.
的“榕树三角形”.
(1)若点![]() 坐标为
坐标为![]() ,且
,且![]() ,则点
,则点![]() 、
、![]() 的“榕树三角形”的面积为 .
的“榕树三角形”的面积为 .
(2)当点![]() 、
、![]() 的“榕树三角形”是等腰三角形时,求点
的“榕树三角形”是等腰三角形时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,作过![]() 、
、![]() 、
、![]() 三点的抛物线
三点的抛物线![]() .
.
①若![]() 点必为抛物线上一点,求点
点必为抛物线上一点,求点![]() 、
、![]() 的“榕树三角形”面积
的“榕树三角形”面积![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
②当点![]() 、
、![]() 的“榕树三角形”面积2,且抛物线
的“榕树三角形”面积2,且抛物线![]() 与点
与点![]() 、
、![]() 的“榕树三角形”恰有两个交点时,直接写出
的“榕树三角形”恰有两个交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD>AB,连接AC,将线段AC绕点A顺时针旋转90得到线段AE,平移线段AE得到线段DF(点A与点D对应,点E与点F对应),连接BF,分别交直线AD,AC于点G,M,连接EF.
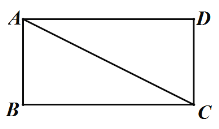
(1) 依题意补全图形;
(2) 求证:EG⊥AD;
(3) 连接EC,交BF于点N,若AB=2,BC=4,设MB=a,NF=b,试比较![]() 与
与![]() 之间的大小关系,并证明.
之间的大小关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在反比例函数
在反比例函数![]() 的图象上,过点
的图象上,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.

(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形的一条边长为x,周长的一半为y,定义(x,y)为这个矩形的坐标。如图2,在平面直角坐标系中,直线x=1,y=3将第一象限划分成4个区域,已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中,则下面叙述中正确的是( )

A. 点A的横坐标有可能大于3
B. 矩形1是正方形时,点A位于区域②
C. 当点A沿双曲线向上移动时,矩形1的面积减小
D. 当点A位于区域①时,矩形1可能和矩形2全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有![]() 名男生,并对两组男生训练前、后引体向上的个数进行统计分析,得到乙组男生训练前、后引体向上的平均个数分别是
名男生,并对两组男生训练前、后引体向上的个数进行统计分析,得到乙组男生训练前、后引体向上的平均个数分别是![]() 个和
个和![]() 个,及下面不完整的统计表和统计图.
个,及下面不完整的统计表和统计图.
甲组男生训练前、后引体向上个数统计表(单位:个)
甲组 | 男生 | 男生 | 男生 | 男生 | 男生 | 男生 | 平均个数 | 众数 | 中位数 |
训练前 |
|
|
|
|
|
|
|
|
|
训练后 |
|
|
|
|
|
|
|
|
|
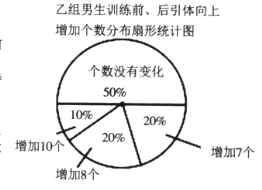
根据以上信息,解答下列问题:
(1)![]() ,
,![]() ,
,![]() ;
;
(2)甲组训练后引体向上的平均个数比训练前增长了 ![]() ;
;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占该组人数的![]() ,所以乙组的平均个数不可能提高
,所以乙组的平均个数不可能提高![]() 个这么多.”你同意他的观点吗?说明理由.
个这么多.”你同意他的观点吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com