
【题目】抛物线![]() 与直线
与直线![]() 交于
交于![]() 两点,且
两点,且![]() 两点之间的抛物线上总有两个纵坐标相等的点.
两点之间的抛物线上总有两个纵坐标相等的点.
(1)求证:![]() ;
;
(2)过![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于
于![]() ,
,![]() ,且当
,且当![]() ,
,![]() ,
,![]() 三点共线时,
三点共线时,![]() 轴.
轴.
①求![]() 的值:
的值:
②对于每个给定的实数![]() ,以
,以![]() 为直径的圆与直线
为直径的圆与直线![]() 总有公共点,求
总有公共点,求![]() 的范围.
的范围.
【答案】(1)见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)先联立 ,消去
,消去![]() 得
得![]() ,法一:根据题意可得出
,法一:根据题意可得出![]() ,从而有
,从而有![]() ,即可得出结果;法二:设这两个纵坐标相等的点的横坐标为
,即可得出结果;法二:设这两个纵坐标相等的点的横坐标为![]() ,
,![]() ,则
,则![]() ,则
,则![]() ,得出
,得出![]() ,从而有
,从而有![]() ,即
,即![]() ,同法一可得出结果;
,同法一可得出结果;
(2)①设![]() ,
,![]() ,根据根与系数的关系可得
,根据根与系数的关系可得![]() ,
,![]() ,由
,由![]() ,
,![]() 均与
均与![]() 轴平行,得出
轴平行,得出![]() ,
,![]() ,由
,由![]() ,
,![]() ,
,![]() 三点共线,有
三点共线,有![]() ,得出
,得出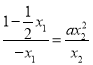 ,即可求出x1,x2,再根据
,即可求出x1,x2,再根据![]() 轴,得出
轴,得出![]() ,将x1,x2代入可求出a的值;②设以
,将x1,x2代入可求出a的值;②设以![]() 为直径的圆与直线
为直径的圆与直线![]() 的公共点为
的公共点为![]() ,连接AP,BP,则
,连接AP,BP,则![]() ,过点A作AM垂直直线y=m于点M,过点B作BN垂直y=m于点N,构造一线三等角,可得:△AMP∽△PNB,得出
,过点A作AM垂直直线y=m于点M,过点B作BN垂直y=m于点N,构造一线三等角,可得:△AMP∽△PNB,得出![]() ,即
,即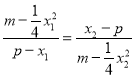 ,整理得
,整理得![]() ,将x1+x2,x1x2代入,然后整理成关于
,将x1+x2,x1x2代入,然后整理成关于![]() 的方程,由
的方程,由![]() 可得出
可得出![]() ,根据题意可得上述不等式对于任意的实数
,根据题意可得上述不等式对于任意的实数![]() 恒成,转化为二次函数
恒成,转化为二次函数![]() 图象开口向上,且与
图象开口向上,且与![]() 轴至多只有一个交点,据此列出关于m的不等式组,解出m即可.
轴至多只有一个交点,据此列出关于m的不等式组,解出m即可.
(1)证明:法一:联立 ,消去
,消去![]() 得
得![]() ,
,
抛物线![]() 的对称轴为
的对称轴为![]() 轴,则这两个纵坐标相等的点关于
轴,则这两个纵坐标相等的点关于![]() 轴对称,
轴对称,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
法二:设这两个纵坐标相等的点的横坐标为![]() ,
,![]() ,
,
则![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() .
.
(2)解:①设![]() ,
,![]() ,
,
则由(1)知![]() ,
,![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() ,
,![]() ,
,
又∵![]() ,
,![]() 均与
均与![]() 轴平行,
轴平行,
∴![]() ,
,![]() ,
,
又∵![]() ,
,![]() ,
,![]() 三点共线,∴
三点共线,∴![]() ,
,
∴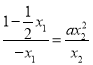 ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() 轴,∴
轴,∴![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
∵![]() ,∴
,∴![]() .
.
②设以![]() 为直径的圆与直线
为直径的圆与直线![]() 的公共点为
的公共点为![]() ,连接AP,BP,则
,连接AP,BP,则![]() ,
,
过点A作AM垂直直线y=m于点M,过点B作BN垂直y=m于点N,构造一线三等角,可得:

△AMP∽△PNB,∴![]() ,∴
,∴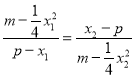 ,
,
∴![]() ,
,
又由①得![]() ,
,![]() ,
,
∴![]() ,
,
将上述方程整理成关于![]() 的方程:
的方程:![]() …(*),
…(*),
∵方程(*)有实数根,
∴![]() ,∴
,∴![]() ,
,
整理得![]() ,
,
对于每个给定的实数![]() ,以
,以![]() 为直径的圆与直线
为直径的圆与直线![]() 总有公共点,即总有点
总有公共点,即总有点![]() 存在,
存在,
∴上述不等式对于任意的实数![]() 恒成.
恒成.
当![]() ,即
,即![]() 时,上述不等式为:
时,上述不等式为:![]() ,舍去;
,舍去;
当![]() 时,欲使上述不等式恒成立,
时,欲使上述不等式恒成立,
则二次函数![]() 图象开口向上,且与
图象开口向上,且与![]() 轴至多只有一个交点,
轴至多只有一个交点,
∴![]() ,解得:
,解得:![]() .
.
∴![]() 的范围为
的范围为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,连接AC、CB,过O作EO∥CB并延长EO到F,使EO=FO,连接AF并延长,AF与CB的延长线交于D.求证:AE2=FGFD.
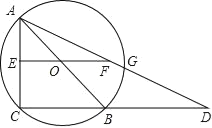
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数![]() 图象的对称轴为
图象的对称轴为![]() 与
与![]() 轴交于点C,与x轴交于点
轴交于点C,与x轴交于点![]() 点
点![]() 给出下列结论:①二次函数的最大值为
给出下列结论:①二次函数的最大值为![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() ;⑤
;⑤![]() 其中正确的个数是( )
其中正确的个数是( )
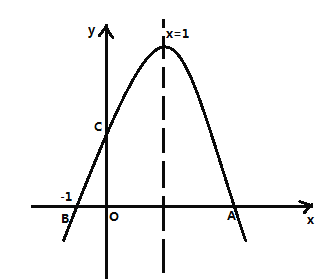
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且DE=FE.
(1)求证:AD为⊙O切线;
(2)若AB=20,tan∠EBA=![]() ,求BC的长.
,求BC的长.
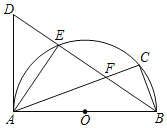
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第![]() 个图中正方形和等边三角形的个数之和为 个.
个图中正方形和等边三角形的个数之和为 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴相交于A、B两点,C(m,﹣3)是图象上的一点,且AC⊥BC,则a的值为( )
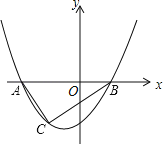
A.2B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2+(m﹣3)x﹣3(m>0)与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,AB=4,点D为抛物线的顶点.
(1)求点A和顶点D的坐标;
(2)将点D向左平移4个单位长度,得到点E,求直线BE的表达式;
(3)若抛物线y=ax2﹣6与线段DE恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
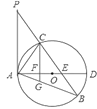
【题目】如图,已知在![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() 是
是![]() 的外接圆,
的外接圆,![]() 是
是![]() 的直径,且交
的直径,且交![]() 于点
于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)在满足(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的半径及
的半径及![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com