
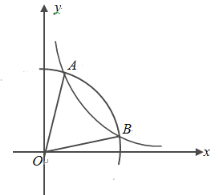
【题目】如图,以点![]() 为圆心,半径为2的圆与
为圆心,半径为2的圆与![]() 的图象交于点
的图象交于点![]() ,若
,若![]() ,则
,则![]() 的值为________.
的值为________.
【答案】1
【解析】
分别过A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,利用对称性,可得∠AOM=∠BON=15°.再作点B关于x轴的对称点C,连接BC,OC,作BD⊥OC于点D,根据S△OBN=![]() S△OBC得出△OBN的面积,从而可求出k的值.
S△OBC得出△OBN的面积,从而可求出k的值.
解:分别过A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,
由圆、反比例函数图象的对称性可知,图形关于一、三象限角平分线对称,即关于直线y=x对称,可得△AOM≌△BON,
∴∠AOM=∠BON=![]() ×(90°-60°)=15°.
×(90°-60°)=15°.
作点B关于x轴的对称点C,连接BC,OC,作BD⊥OC于点D,
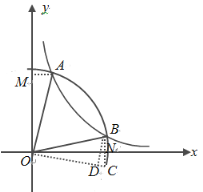
则∠BOC=2∠BON=30°,OB=OC=2,
∴BD=![]() OB=1,
OB=1,
∴S△OBN=![]() S△OBC=
S△OBC=![]() ×OC×BD=1,
×OC×BD=1,
∴k=S△OBN=1.
故答案为:1.


科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为22m,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为( )
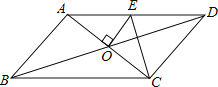
A. 8cmB. 9cmC. 10cmD. 11cm
查看答案和解析>>
科目:初中数学 来源: 题型:
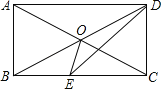
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与直线
与直线![]() 交于
交于![]() 两点,且
两点,且![]() 两点之间的抛物线上总有两个纵坐标相等的点.
两点之间的抛物线上总有两个纵坐标相等的点.
(1)求证:![]() ;
;
(2)过![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于
于![]() ,
,![]() ,且当
,且当![]() ,
,![]() ,
,![]() 三点共线时,
三点共线时,![]() 轴.
轴.
①求![]() 的值:
的值:
②对于每个给定的实数![]() ,以
,以![]() 为直径的圆与直线
为直径的圆与直线![]() 总有公共点,求
总有公共点,求![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD>AB,连接AC,将线段AC绕点A顺时针旋转90得到线段AE,平移线段AE得到线段DF(点A与点D对应,点E与点F对应),连接BF,分别交直线AD,AC于点G,M,连接EF.
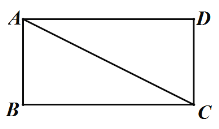
(1) 依题意补全图形;
(2) 求证:EG⊥AD;
(3) 连接EC,交BF于点N,若AB=2,BC=4,设MB=a,NF=b,试比较![]() 与
与![]() 之间的大小关系,并证明.
之间的大小关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com