
【题目】菱形![]() 中,
中,![]() 为边
为边![]() 上的点,
上的点,![]() 相交于点
相交于点![]() .
.
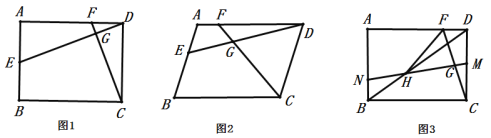
(1)如图1,若![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() .求证:
.求证:![]() ;
;
(3)如图3,在(1)的条件下,平移线段![]() 到
到![]() ,使
,使![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
【答案】(1)见解析;(2)见解析;(3)1+![]() .
.
【解析】
(1)由菱形ABCD中和∠A=90°可得菱形ABCD是正方形,根据正方形性质得AD=DC,∠A=∠CDF=90°,再加上DE=CF即证得Rt△ADE≌Rt△DCF,所以∠ADE=∠DCF,等量代换计算即得到∠CGD=90°,得证.
(2)由菱形性质可得AD=CD,∠B=∠ADC,∠B+∠BAD=180°,再由∠EGC+∠B=180°可得∠A=∠EGC=∠DGF,∠CGD=∠B=∠ADC,证明△ADE∽△GDF和△DCG∽△FCD,再由对应边成比例等量代换计算得DE=CF.
(3)由(1)的条件可得MN=CF,MN⊥CF,加上G为CF的中点,即MN垂直平分CF,连接FM即有FM=MC且∠DMF=∠MFC+∠FCD=30°,设DF=x,则根据30°直角三角形的性质,可用x表示FM、DM.过点N作CD的垂线段NP,则CP=BN=![]() ,且易证Rt△NPM≌Rt△CDF,所以MP=DF=x,进而能用x表示CM、CD.利用MF=MC列出关于x的方程,求解即得到CM、CD、DF的长.证明△CGM∽△CDF,根据对应边成比例计算即求得FG=CG的长.
,且易证Rt△NPM≌Rt△CDF,所以MP=DF=x,进而能用x表示CM、CD.利用MF=MC列出关于x的方程,求解即得到CM、CD、DF的长.证明△CGM∽△CDF,根据对应边成比例计算即求得FG=CG的长.
解:(1)证明:∵菱形ABCD中,∠A=90°
∴菱形ABCD是正方形
∴AD=DC,∠A=∠CDF=90°
在Rt△ADE与Rt△DCF中
DE=CF,AD=DC,
∴Rt△ADE≌Rt△DCF(HL)
∴∠ADE=∠DCF
∴∠DCF+∠CDE=∠ADE+∠CDE=∠ADC=90°
∴∠CGD=90°
∴DE⊥CF
(2)证明:∵四边形ABCD是菱形
∴AD=CD,∠B=∠ADC,AD∥BC
∴∠A+∠B=180°
∵∠EGC+∠B=180°,∠EGC+∠CGD=180°
∴∠A=∠EGC=∠DGF,∠CGD=∠B=∠ADC
∵∠A=∠DGF,∠ADE=∠GDF
∴△ADE∽△GDF
∴![]() ,
,
∴![]()
∵∠CGD=∠CDF,∠DCG=∠FCD
∴△DCG∽△FCD
∴![]() ,
,
∴![]() ,
,
∵AD=DC,
∴DE=CF;
(3)如图,过点N作NP⊥CD于点P,连接FM,
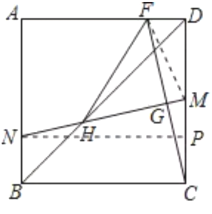
∴∠CPN=∠MPN=90°,
∵四边形ABCD是正方形
∴∠ABC=∠BCD=∠ADC=90°,BC=CD
∴四边形BCPN是矩形
∴NP=BC=CD,PC=BN=![]() ,
,
在Rt△NPM与Rt△CDF中
MN=CF,NP=CD,
∴Rt△NPM≌Rt△CDF(HL)
∴PM=DF
设PM=DF=x,则CM=PC+PM=![]() +x,
+x,
∵由(1)得MN⊥CF,G为CF中点
∴MN垂直平分CF
∴MF=MC
∴∠MFC=∠FCD=15°
∴∠DMF=∠MFC+∠FCD=30°
∴Rt△DMF中,MF=2DF=2x,DM=![]() ,
,
由于MF=MC,即2x=![]() +x
+x
∴x=![]()
∴DF=![]() ,DM=
,DM=![]() ,CM=MF=2
,CM=MF=2![]() ,CD=CM+DM=2
,CD=CM+DM=2![]() +
+![]()
∵∠GCM=∠MCF,∠CGM=∠CDF=90°
∴△CGM∽△CDF
∴![]() ,
,
∴2CG2=CDCM=(2![]() +
+![]() )2
)2![]() =8+4
=8+4![]() ,
,
∴CG2=4+2![]() =12+2
=12+2![]() +(
+(![]() )2=(1+
)2=(1+![]() )2,
)2,
∴FG=CG=1+![]() .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB.CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
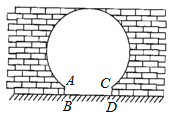
A.2米 B.2.5米 C.2.4米 D.2.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将从1开始的连续自然数按图规律排列:
列 行 | 第1列 | 第2列 | 第3列 | 第4列 |
第1行 | 1 | 2 | 3 | 4 |
第2行 | 8 | 7 | 6 | 5 |
第3行 | 9 | 10 | 11 | 12 |
第4行 | 16 | 15 | 14 | 13 |
… | … | … | … | … |
第 | … | … | … | … |
规定位于第![]() 行,第
行,第![]() 列的自然数10记为
列的自然数10记为![]() ,自然数15记为
,自然数15记为![]() …按此规律,自然数2018记为______.
…按此规律,自然数2018记为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:宽与长的比是![]() (约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:
(约为0.618)的矩形叫作黄金矩形.黄金矩形给我们以协调、匀称的美感,世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形(提示:![]() ).
).
第一步:在矩形纸片一端 ,利用图1的方法折出一个正方形,然后把纸片展平;
第二步:如图2,把这个正方形折成两个相等的矩形,再把纸片展平;
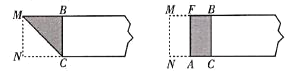
图1 图2
第三步:折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处;
处;
第四步:展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ,则图4中就会出现黄金矩形.
,则图4中就会出现黄金矩形.
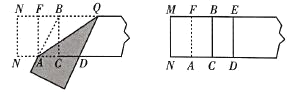
图3 图4
(1)在图3中![]() _________ (保留根号);
_________ (保留根号);
(2)如图3,则四边形![]() 的形状是_________;
的形状是_________;
(3)在图4中黄金矩形是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 边上的两点,且
边上的两点,且![]() 分别交
分别交![]() 于
于![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]()
![]() .其中正确的结论是( )
.其中正确的结论是( )
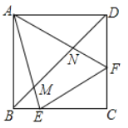
A.②③④B.①④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2ax+c(a<0)的图象过点A(3,m).
(1)当a=﹣1,m=0时,求抛物线的顶点坐标_____;
(2)如图,直线l:y=kx+c(k<0)交抛物线于B,C两点,点Q(x,y)是抛物线上点B,C之间的一个动点,作QD⊥x轴交直线l于点D,作QE⊥y轴于点E,连接DE.设∠QED=β,当2≤x≤4时,β恰好满足30°≤β≤60°,a=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
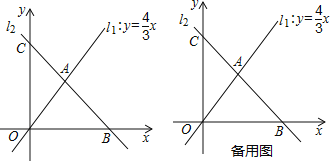
【题目】如图,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() .
.
(1)求直线![]() 的关系式;
的关系式;
(2)若与![]() 轴平行的直线
轴平行的直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、点
、点![]() ,则
,则![]() 的面积为_____(直接填空);
的面积为_____(直接填空);
(3)在(2)的情况下,把![]() 沿着过原点的直线
沿着过原点的直线![]() 翻折,当点
翻折,当点![]() 落在直线
落在直线![]() 上时,直接写出
上时,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com