
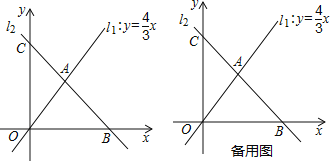
【题目】如图,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() .
.
(1)求直线![]() 的关系式;
的关系式;
(2)若与![]() 轴平行的直线
轴平行的直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、点
、点![]() ,则
,则![]() 的面积为_____(直接填空);
的面积为_____(直接填空);
(3)在(2)的情况下,把![]() 沿着过原点的直线
沿着过原点的直线![]() 翻折,当点
翻折,当点![]() 落在直线
落在直线![]() 上时,直接写出
上时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)14;(3)
;(2)14;(3)![]() 或
或![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A的坐标,由点A的坐标,再利用待定系数法即可求出直线l2的解析式;
(2)利用一次函数图象上点的坐标特征可求出点B,M,N的坐标,再利用三角形的面积公式即可求出△BMN的面积;
(3)设翻折后点A落在点F处,连接AF交折线于点P,由折痕所在直线的解析式可设直线AF的解析式为y=-![]() x+d,由点A的坐标,利用待定系数法可求出直线AF的解析式,代入x=8可求出点F的坐标,由折叠的性质结合点A,F的坐标可求出点P的坐标,再利用一次函数图象上点的坐标特征可得出关于k的方程,解之即可得出结论.
x+d,由点A的坐标,利用待定系数法可求出直线AF的解析式,代入x=8可求出点F的坐标,由折叠的性质结合点A,F的坐标可求出点P的坐标,再利用一次函数图象上点的坐标特征可得出关于k的方程,解之即可得出结论.
(1)将A(6,a)代入y=![]() x,得:a=
x,得:a=![]() ×6,
×6,
∴a=8,
∴点A的坐标为(6,8).
将A(6,8)代入y=-x+b,得:8=-6+b,
∴b=14,
∴直线l2的解析式为y=-x+14.
(2)当x=8时,y=![]() x=
x=![]() ,y=-x+14=6,
,y=-x+14=6,
∴点M的坐标为(8,![]() ),点N的坐标为(8,6).
),点N的坐标为(8,6).
当y=0时,-x+14=0,
解得:x=14,
∴点B的坐标为(14,0).
设直线x=8与x轴的交点为E,则点E的坐标为(8,0),如图1所示.

∴S△BMN=![]() BEMN=
BEMN=![]() ×(14-8)×(
×(14-8)×(![]() -6)=14.
-6)=14.
故答案为14.
(3)设翻折后点A落在点F处,连接AF交折痕所在的直线于点P,如图2所示.
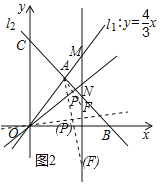
∵折痕所在直线的解析式为y=kx(k≠0),
∴设直线AF的解析式为y=-![]() x+d,
x+d,
将A(6,8)代入y=-![]() x+d,得:8=-
x+d,得:8=-![]() +d,
+d,
∴d=8+![]() ,
,
∴直线AF的解析式为y=-![]() x+8+
x+8+![]() .
.
当x=8时,y=-![]() x+8+
x+8+![]() =8-
=8-![]() ,
,
∴点F的坐标为(8,8-![]() ).
).
又∵点P为线段AF的中点,
∴点P的坐标为(![]() ,
, ),即(7,8-
),即(7,8-![]() ).
).
将P(7,8-![]() )代入y=kx,得:8-
)代入y=kx,得:8-![]() =7k,
=7k,
整理,得:7k2-8k+1=0,
解得:k1=1,k2=![]() ,
,
∴k的值为1或![]() .
.


科目:初中数学 来源: 题型:
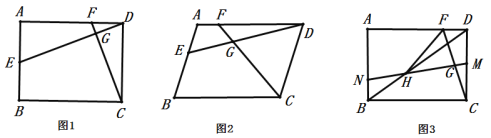
【题目】菱形![]() 中,
中,![]() 为边
为边![]() 上的点,
上的点,![]() 相交于点
相交于点![]() .
.
(1)如图1,若![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() .求证:
.求证:![]() ;
;
(3)如图3,在(1)的条件下,平移线段![]() 到
到![]() ,使
,使![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“危险废物”,处理不当将污染环境,危害健康某市药监部门为了解家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.
(1)下列选取样本的方法最合理的一种是 (只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如下图:
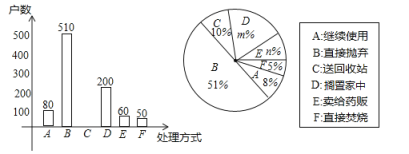
①![]() ,
,
②补全条形统计图;(标上数据)
③家庭过期药品的正确处理方式是送回收站,若该市有![]() 万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中学生对待学习的态度一直是教育工作者极为关注的一个问题.为此某市教育局对本市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:喜欢;B级:不太喜欢;C级:不喜欢),并将调查结果绘制成不完整的统计图(如图![]() ).请根据图中提供的信息,解答下列问题:
).请根据图中提供的信息,解答下列问题:
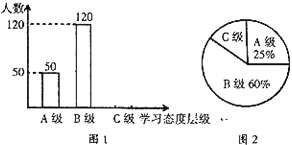
(1)此次抽样调查中,共调查了_____名学生;
(2)将条形统计图补充完整;
(3)求出扇形统计图中![]() 级所占的圆心角的度数;
级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该市近![]() 名初中生中大约有多少名学生学习态度达标.(达标包括
名初中生中大约有多少名学生学习态度达标.(达标包括![]() 级和
级和![]() 级)
级)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是直线
是直线![]() 上的两点,直线l1、l2的初始位置与直线
上的两点,直线l1、l2的初始位置与直线![]() 重合将l1绕点
重合将l1绕点![]() 顺时针以每秒10°的速度旋转,将l2绕点B逆时针以每秒5°的速度旋转,且两条直线从重合位置同时开始旋转,设旋转时间为
顺时针以每秒10°的速度旋转,将l2绕点B逆时针以每秒5°的速度旋转,且两条直线从重合位置同时开始旋转,设旋转时间为![]() 秒(
秒(![]() 是正整数).当
是正整数).当![]() 时,设
时,设![]() 的交点为
的交点为![]() ;当
;当![]() 时,设
时,设![]() 的交点为
的交点为![]() ;当
;当![]() 时设
时设![]() 的交点为
的交点为![]() ……那么当
……那么当![]() 时,
时, ![]() 相交所得的钝角是__________.当
相交所得的钝角是__________.当![]() 落在
落在![]() 上方时,
上方时, ![]() 的最小值是__________.
的最小值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂的甲、乙两个车间各生产了400个新款产品,为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围在165≤x<180为合格),分别从甲、乙两个车间生产的产品中随机各抽取了20个样品迸行检测,获得了它们的数据(尺寸),并对数据进行了整理、描述和分析.下面给出了部分信息:
a.甲车间产品尺寸的扇形统计图如下(数据分为6组:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲车间生产的产品尺寸在175≤x<180这一组的是:
175 176 176 177 177 178 178 179 179
c.甲、乙两车间生产产品尺寸的平均数、中位数、众数如下:
车间 | 平均数 | 中位数 | 众数 |
甲车间 | 178 | m | 183 |
乙车间 | 177 | 182 | 184 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)此次检测中,甲、乙两车间生产的产品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假设这个工厂生产的所有产品都参加了检测,那么估计甲车间生产该款新产品中合格产品有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com