Question

【题目】已知直线y=kx+b与抛物线y=ax2（a＞0）相交于A、B两点（点A在点B的左侧），与y轴正半轴相交于点C，过点A作AD⊥x轴，垂足为D．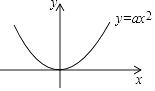

（1）若∠AOB=60°，AB∥x轴，AB=2，求a的值；
（2）若∠AOB=90°，点A的横坐标为﹣4，AC=4BC，求点B的坐标；
（3）延长AD、BO相交于点E，求证：DE=CO．

Answer 1

【答案】
（1）解：如图1，

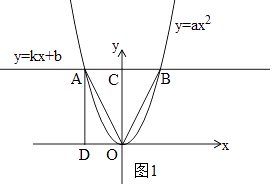
∵抛物线y=ax2的对称轴是y轴，且AB∥x轴，

∴A与B是对称点，O是抛物线的顶点，

∴OA=OB，

∵∠AOB=60°，

∴△AOB是等边三角形，

∵AB=2，AB⊥OC，

∴AC=BC=1，∠BOC=30°，

∴OC= ，

∴A（﹣1， ），

把A（﹣1， ）代入抛物线y=ax2（a＞0）中得：a= ；

（2）解：如图2，过B作BE⊥x轴于E，过A作AG⊥BE，交BE延长线于点G，交y轴于F，

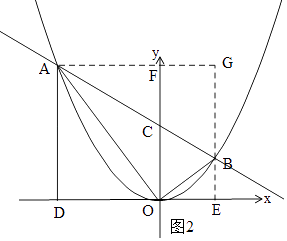
∵CF∥BG，

∴ ，

∵AC=4BC，

∴ =4，

∴AF=4FG，

∵A的横坐标为﹣4，

∴B的横坐标为1，

∴A（﹣4，16a），B（1，a），

∵∠AOB=90°，

∴∠AOD+∠BOE=90°，

∵∠AOD+∠DAO=90°，

∴∠BOE=∠DAO，

∵∠ADO=∠OEB=90°，

∴△ADO∽△OEB，

∴ ，

∴ ，

∴16a2=4，

a=± ，

∵a＞0，

∴a= ；

∴B（1， ）；

（3）解：如图3，

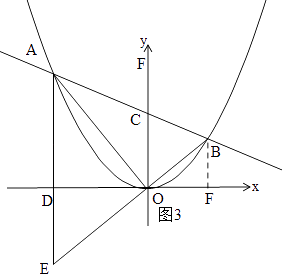
设AC=nBC，由（2）同理可知：A的横坐标是B的横坐标的n倍，

则设B（m，am2），则A（﹣mn，am2n2），

∴AD=am2n2，

过B作BF⊥x轴于F，

∴DE∥BF，

∴△BOF∽△EOD，

∴ = = ，

∴ ，

∴ = ，DE=am2n，

∴ = ，

∵OC∥AE，

∴△BCO∽△BAE，

∴ ，

∴ = ，

∴CO= =am2n，

∴DE=CO．

【解析】（1）过等边三角形的内心分别作三边的平行线，求a的值；
（2）如图2，作辅助线，构建平行线和相似三角形，根据CF∥BG，由A的横坐标为-4，得B的横坐标为1，所以A（-4，16a），B（1，a），证明△ADO∽△OEB，即可得到所求结论；
（3）如图3，设AC=nBC由（2）同理可知：A的横坐标是B的横坐标的n倍，分别根据两三角形相似计算DE和CO的长即可得出DE=CO．