
【题目】已知a=﹣(﹣2)2×3,b=|﹣9|+(﹣7),c=(![]() )÷
)÷![]() .
.
(1)求2[a﹣(b+c)]﹣[b﹣(a﹣2c)]的值.
(2)若A=(﹣![]() )2÷(﹣
)2÷(﹣![]() )+(1﹣
)+(1﹣![]() )2×(1﹣3)2,B=|a|﹣5b+2c,试比较A和B的大小.
)2×(1﹣3)2,B=|a|﹣5b+2c,试比较A和B的大小.
(3)如图,已知点D是线段AC的中点,点B是线段DC上的一点,且CB:BD=2:3,若AB═![]() cm,求BC的长.
cm,求BC的长.
![]()
【答案】(1)﹣34;(2)A=B;(3)BC=0.25cm.
【解析】
(1)先计算出a、b、c的值,然后把值代入化简后的代数式;(2)注意负数的乘方运算和基本的有理数的运算;(3)灵活的应用中点,从比例因为未知数建立方程,将线段问题转为方程问题.
(1)a=﹣4×3=﹣12,b=9﹣7=2,c=﹣2
原式=2a﹣2(b+c)﹣b+(a﹣2c)=3a﹣3b﹣4c
当a=﹣12,b=2,c=﹣2时,原式=3×(﹣12)﹣3×2﹣4×(﹣2)=﹣34
(2)A=![]() ×(﹣27)+
×(﹣27)+ ![]() ×4=﹣2,B=12﹣5×2+2×(﹣2)=﹣2,∴A=B
×4=﹣2,B=12﹣5×2+2×(﹣2)=﹣2,∴A=B
(3)AB=![]() =1(cm),
=1(cm),
设CB=2x,BD=3x,则DC=CB+BD=5x
∵点D是线段AC的中点,
∴AD=DC=5x,AB=8x
则8x=1,x=![]() ,BC=
,BC=![]() cm.
cm.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD= ![]() ,请求出AC的长.
,请求出AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC 中,∠A=60°,∠ACB=40°,D为BC边延长线上一点,BM平分∠ABC,E为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求∠BEC的度数;
②若CE平分∠ACD,求∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
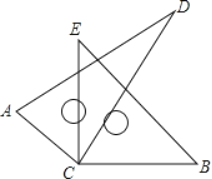
【题目】如图,将两块直角三角板的直角顶点C叠放在一起.
(1)若∠DCE=28°10',求∠ACB的度数;
(2)若∠ACB=148°21',求∠DCE的度数;
(3)直接写出∠ACB与∠DCE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A、B、C,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取.用画树状图或列表的方法列出所有等可能的结果,并求甲、乙抽中同一篇文章的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)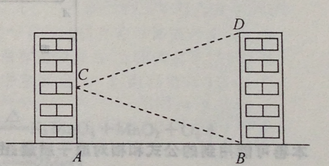
(1)求∠BCD的度数.
(2)求教学楼的高BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A,B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜种植农户购买白菜苗和西红柿苗共1000株,其中白菜苗每株3元,西红柿苗每株5元.已知该农户打算用不少于3600元但不多于3800元的资金购买两种蔬菜.
(1)求该农户可以购买白菜苗株数的最大值和最小值;
(2)该农户按(1)中购买白菜苗株数的最小值的方案购买两种蔬菜苗,经过农户的精心培育,两种蔬菜苗全成活.根据以往的数据分析,平均一株白菜苗可长成2千克白菜,平均一株西红柿苗可结3千克西红柿.农户计划采用直接销售和生态采摘销售两种方式进行销售,其中直接销售白菜的售价为每千克4元,直接销售西红柿的售价为每千克5元;生态采摘销售时两种蔬菜的售价一样,都比直接销售白菜的售价高![]() ,但生态采摘过程中会有
,但生态采摘过程中会有![]() 的损耗.当白菜和西红柿各直接销售一半后、剩下的全部采用生态采摘销售时,该农户可获得8080元的利润.求
的损耗.当白菜和西红柿各直接销售一半后、剩下的全部采用生态采摘销售时,该农户可获得8080元的利润.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.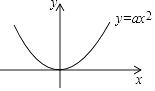
(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;
(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;
(3)延长AD、BO相交于点E,求证:DE=CO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com