
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD= ![]() ,请求出AC的长.
,请求出AC的长.
【答案】
(1)解:连接OC, 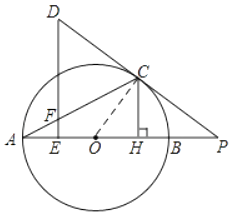
∵∠COB=2∠A,∠D=2∠A
∴∠COB=∠D,
∵DE⊥AP,
∴∠DEP=90°,
在Rt△DEP中,∠DEP=90°,
∴∠P+∠D=90°
∴∠P+∠COB=90°,
∴∠OCP=90°,
∴半径OC⊥DC,
∴DC与⊙O相切
(2)解:由(1)可知:∠OCP=90°,∠COP=∠D,
∴cos∠COP=cos∠D= ![]() ,
,
∵CH⊥OP
∴∠CHO=90°,
设⊙O的半径为r,
则OH=r﹣2
在Rt△CHO中,
cos∠HOC= ![]() =
= ![]() =
= ![]()
∴r=5
∴OH=5﹣2=3
∴由勾股定理可知:CH=4,
∴AH=AB﹣HB=10﹣2=8
在Rt△AHC中,∠CHA=90°,
∴由勾股定理可知:AC=4 ![]()
【解析】(1)证切线可连结半径,证垂直;(2)转化cos∠COP=cos∠D,在Rt△CHO中利用三角函数列方程求出r从而求出AC.
【考点精析】根据题目的已知条件,利用勾股定理的概念和直线与圆的三种位置关系的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,Rt△ACB 中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
(1)利用直尺和圆规在图1中画出⊙O(不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);
(2)判断BD所在直线与(1)中所作的⊙O的位置关系,并证明你的结论;
(3)设⊙O交AB于点E,连接DE,过点E作EF⊥BC,F为垂足,若点D是线段AC的黄金分割点(即 ![]() =
= ![]() ),如图2,试说明四边形DEFC是正方形).
),如图2,试说明四边形DEFC是正方形).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和36,求△EDF的面积________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm2,则四边形PFCG的面积为_______cm2.
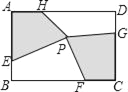
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点坐标分别为A(﹣6,3),B(﹣4,1),C(﹣1,1).
(1)如图1,顺次连接AB,BC,CA,得△ABC.
①点A关于x轴的对称点A1的坐标是 , 点B关于y轴的对称点B1的坐标是;
②画出△ABC关于原点对称的△A2B2C2;
③tan∠A2C2B2=;
(2)利用四边形的不稳定性,将第二象限部分由小正方形组成的网格,变化为如图2所示的由小菱形组成的网格,每个小菱形的边长仍为1个单位长度,且较小内角为60°,原来的格点A,B,C分别对应新网格中的格点A′,B′,C′,顺次连接A′B′,B′C′,C′A′,得△A′B′C′,则tan∠A′C′B′= . 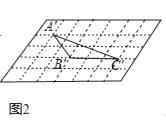
查看答案和解析>>
科目:初中数学 来源: 题型:
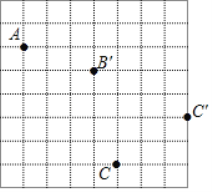
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出来点A,点B′、点C和它的对应点C′.
(1)请画出平移前后的△ABC和△A′B′C′;(注意并标注好字母)
(2)利用网格画出△ABC中BC边上的中线AD;(注意并标注好字母)
(3)利用网格画出△ABC中AB边上的高CE;(注意并标注好字母)
(4)△A′B′C′的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产上第世博会吉祥物:“海宝”纪念章10万个,质检部门为检测这批纪念章质量的合格情况,从中随机抽查500个,合格499个![]() 下列说法正确的是
下列说法正确的是![]()
![]()
A. 总体是10万个纪念章的合格情况,样本是500个纪念章的合格情况
B. 总体是10万个纪念章的合格情况,样本是499个纪念章的合格情况
C. 总体是500个纪念章的合格情况,样本是500个纪念章的合格情况
D. 总体是10万个纪念章的合格情况,样本是1个纪念章的合格情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=﹣(﹣2)2×3,b=|﹣9|+(﹣7),c=(![]() )÷
)÷![]() .
.
(1)求2[a﹣(b+c)]﹣[b﹣(a﹣2c)]的值.
(2)若A=(﹣![]() )2÷(﹣
)2÷(﹣![]() )+(1﹣
)+(1﹣![]() )2×(1﹣3)2,B=|a|﹣5b+2c,试比较A和B的大小.
)2×(1﹣3)2,B=|a|﹣5b+2c,试比较A和B的大小.
(3)如图,已知点D是线段AC的中点,点B是线段DC上的一点,且CB:BD=2:3,若AB═![]() cm,求BC的长.
cm,求BC的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com