
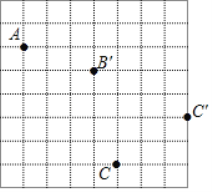
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出来点A,点B′、点C和它的对应点C′.
(1)请画出平移前后的△ABC和△A′B′C′;(注意并标注好字母)
(2)利用网格画出△ABC中BC边上的中线AD;(注意并标注好字母)
(3)利用网格画出△ABC中AB边上的高CE;(注意并标注好字母)
(4)△A′B′C′的面积为 .
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足|a-![]() |+
|+![]() +(c-
+(c-![]() )2=0.
)2=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能,求出其周长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)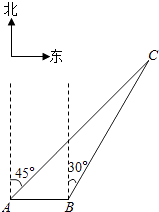
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校想知道九年级学生对我国倡导的“一带一路”的了解程度,随机抽取部分九年级学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):A.非常了解.B.了解.C.知道一点.D.完全不知道.将调查的结果绘制如下两幅不完整的统计图,请根据两幅统计图中的信息,解答下列问题: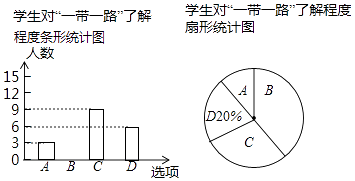
(1)求本次共调查了多少学生?
(2)补全条形统计图;
(3)该校九年级共有600名学生,请你估计“了解”的学生约有多少名?
(4)在“非常了解”的3人中,有2名女生,1名男生,老师想从这3人中任选两人做宣传员,请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD= ![]() ,请求出AC的长.
,请求出AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
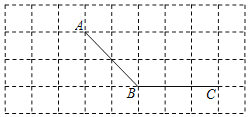
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ![]() ≈1.414)( )
≈1.414)( )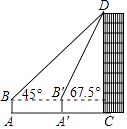
A.34.14米
B.34.1米
C.35.7米
D.35.74米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】物理兴趣小组20位同学在实验操作中的得分情况如下表:(Ⅰ)求这组数据的众数、中位数;(Ⅱ)求这组数据的平均数;(Ⅲ)将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
得分(分) | 10 | 9 | 8 | 7 |
人数(人) | 5 | 8 | 4 | 3 |
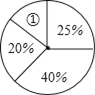
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)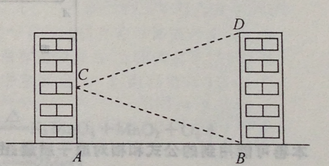
(1)求∠BCD的度数.
(2)求教学楼的高BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com