练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．某天的最高气温是11℃，最低气温是-1℃，则这一天的最高气温与最低气温的差是（　　）
    A．2℃B．-2℃C．12℃D．-12℃

    分析 用最高温度减去最低温度，然后根据减去一个数等于加上这个数的相反数进行计算即可得解．

    解答 解：11-（-1），
    =11+1，
    =12（℃）．
    故选C．

    点评 本题考查了有理数的减法，是基础题，熟记减去一个数等于加上这个数的相反数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．小明家、学校与图书馆依次在一条直线上，小明、小亮两人同时分别从小明家和学校出发沿直线匀速步行到图书馆借阅图书，小明到达图书馆花了20分钟，小亮每分钟步行40米，小明离学校的距离y（米）与两人出发时间x（分）之间的函数图象如图所示．
    （1）小明每分钟步行60米，a=960，小明家离图书馆的距离为1200米．
    （2）在图中画出小亮离学校的距离y（米）与x（分）之间的函数图象．
    （3）求小明和小亮在途中相遇时二人离图书馆的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．计算$\sqrt{12}×\sqrt{\frac{1}{3}}+\sqrt{5}×\sqrt{3}$的结果在（　　）
    A．4至5之间B．5至6之间C．6至7之间D．7至8之间

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

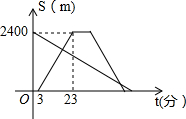    7．小红从劳动基地出发，步行返回学校，小军骑车从学校出发去劳动基地，在基地停留10分钟后，沿原路以原速返回，结果比小红早7分钟回到学校，若两人都是沿着同一路线行进，且两人与学校的距离s（米）和小红从劳动基地出发所用时间t（分）之间的函数关系如图所示，则下列说法中正确的结论有（　　）个
    ①学校到劳动基地距离是2400米；
    ②小军出发53分钟后回到学校；
    ③小红的速度是40米/分；
    ④两人第一次相遇时距离学校1610米．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求代数式$\frac{a+1}{a-2}$÷（a+2-$\frac{3}{2-a}$）的值，其中a=tan45°+2sin60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．爸爸给双胞胎兄弟小明和小强带回一张篮球比赛门票，兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球，各自设计一种游戏确定谁去．
    小明：A袋中放着分别标有数字1、2、3的三个小球，B袋中放着分别标有数字4、5 的两个小球，且都已各自搅匀，小强蒙上眼睛从两个口袋中各取出1个小球，若两个小球上的数字之积为偶数，则小明得到门票；若积为奇数，则小强得到门票．
    小强：口袋中放着分别标有数字1、2、3的三个小球，且已搅匀，小明、小强各蒙上眼睛有放回地摸1次，小明摸到偶数就记2分，摸到奇数记0分；小强摸到奇数就记1分，摸到偶数记0分，积分多的就得到门票（若积分相同，则重复第二次）．
    （1）小明设计的游戏方案对双方是否公平？请你运用列表或树状图说明理由；
    （2）小强设计的游戏方案对双方是否公平？不必说理．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

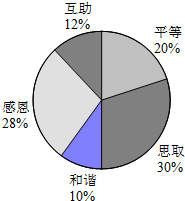    11．某校开展了以“人生观、价值观”为主题的班会活动，活动结束后，初三（1）班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查（要求每位同学只选自己最认可的一项观点），并制成了如下扇形统计图．
    （1）该班学生选择“和谐”观点的有5人，在扇形统计图中，“和谐”观点所在扇形区域的圆心角是36°
    （2）如果该校有400名初三学生，利用样本估计选择“感恩”观点的初三学生约有112人．
    （3）如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查，求恰好选到“和谐”和“感恩”观点的概率．（用树状图或列表法分析解答）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

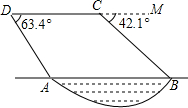    8．如图，某勘测飞机为了测量一湖泊两端A，B的距离，飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°，然后沿着平行于AB的方向水平飞行了125米，在点D测得端点B的俯角为42.1°，求湖泊A、B两端的距离．（参考数据：tan63.4°≈2.00，sin63.4°≈0.89，cos63.4°≈0.45，tan42.1°≈0.90，sin42.1°≈0.67，cos42.1°≈0.74．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．某商场同时购进甲、乙两种商品共200件，其进价和售价如下表，
    商品名称甲乙
    进价（元/件）80100
    售价（元/件）160240
    设其中甲种商品购进x件
    （1）若该商场购进这200件商品恰好用去17900元，求购进甲、乙两种商品各多少件？
    （2）若设该商场售完这200件商品的总利润为y元．
    ①求y与x的函数关系式；
    ②该商品计划最多投入18000元用于购买这两种商品，则至少要购进多少件甲商品？若售完这些商品，则商场可获得的最大利润是多少元？
    （3）实际进货时，生产厂家对甲种商品的出厂价下调a元（50＜a＜70）出售，且限定商场最多购进120件，若商场保持同种商品的售价不变，请你根据以上信息及（2）中的条件，设计出使该商场获得最大利润的进货方案．

    查看答案和解析>>

    同步练习册答案