
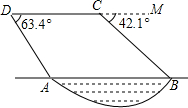
 如图,某勘测飞机为了测量一湖泊两端A,B的距离,飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.(参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.)
如图,某勘测飞机为了测量一湖泊两端A,B的距离,飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.(参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.) 分析 过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,利用三角函数求出AF的长,在Rt△BDF中,利用三角函数求出BE的长,进而可得AB的长.
解答  解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
由题意可得∠ADC=63.4°,∠MDB=42.1°,CD=EF=125米,CE=DF=90米,
在Rt△ADF中,∠DAF=∠ACD=63.4°,
∵tan63.4°=$\frac{DF}{AF}$≈2.00,
∴AF=≈$\frac{90}{2.00}$=45米,
在Rt△BCE中,∠CBE=∠MDB=42.1°,
∵tan42.1°=$\frac{CE}{BE}$≈2.00,
∴BE=≈$\frac{90}{0.90}$=100米,
∴AB=EF-AF+BE=125-45+100=180米.
答:湖泊A、B两端的距离为180米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
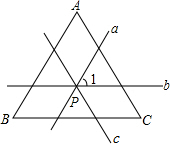 如图,P为△ABC内任意一点,过点P分别画a∥AB,b∥BC,c∥AC.那么只要再给出∠A、∠B、∠C三个角中哪一个角的度数,即可求得∠1的度数?试说明你的理由.
如图,P为△ABC内任意一点,过点P分别画a∥AB,b∥BC,c∥AC.那么只要再给出∠A、∠B、∠C三个角中哪一个角的度数,即可求得∠1的度数?试说明你的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com