
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
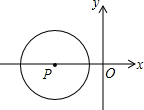 如图,平面直角坐标中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相交,则平移的距离d的取值范围是1<d<5.
如图,平面直角坐标中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相交,则平移的距离d的取值范围是1<d<5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
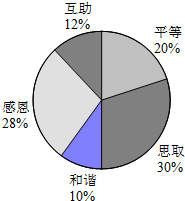 某校开展了以“人生观、价值观”为主题的班会活动,活动结束后,初三(1)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
某校开展了以“人生观、价值观”为主题的班会活动,活动结束后,初三(1)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.36×102 | B. | 0.36×103 | C. | 3.6×102 | D. | 3.6×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
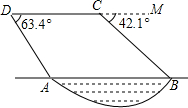 如图,某勘测飞机为了测量一湖泊两端A,B的距离,飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.(参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.)
如图,某勘测飞机为了测量一湖泊两端A,B的距离,飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.(参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
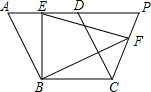 如图,在平行四边形ABCD,BE⊥AD于点E,且点E为AD中点,tanA=2,点P在AD的延长线上,作EF⊥CP于点F,连接BF.
如图,在平行四边形ABCD,BE⊥AD于点E,且点E为AD中点,tanA=2,点P在AD的延长线上,作EF⊥CP于点F,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com