
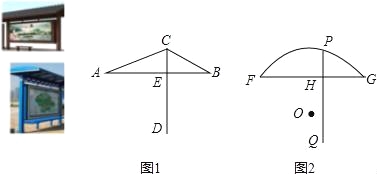
����Ŀ�����г��з�ò�����������ڻ��Ƚ����У�����з���һЩ�ƾɵĹ�������ͤ�а���հ����������һ���µĹ�������ͤ���鿴�����ϵ�һЩ��ͤͼƬ�����ʦ������������ʾ��ͼ��AB��FG��Ϊˮƽ�߶Σ�CD��AB��PQ��FG��E��HΪ���㣬��AE=FH��AB=FG=2����ͼ1��tanA=![]() ��tanB=
��tanB=![]() ��ͼ2��P�ڻ�FG�ϣ��һ�FG����Բ��Բ��O��FG��PQ�ľ���֮��Ϊ5��2��
��ͼ2��P�ڻ�FG�ϣ��һ�FG����Բ��Բ��O��FG��PQ�ľ���֮��Ϊ5��2��
��1����ͼ1�е�CE����
��2����ͼ2�е�PH����
���𰸡���1��0.48��2��0.6
��������
�����������1���ȸ�����֪�����ó�![]() AE=
AE=![]() BE���ٸ���AE+BE=2�����AE�ij���������CE�ij����ɣ�
BE���ٸ���AE+BE=2�����AE�ij���������CE�ij����ɣ�
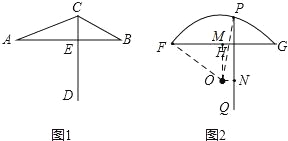
��2��������OF��OP������O��FG�Ĵ��ߣ���PQ�Ĵ��ߣ�����ֱ�������Σ��ٸ��ݹ��ɶ������OF�ij��������õ�OP���������ݹ��ɶ������PN�ij������������߶εĺͲ��ϵ�õ�PH�ij���
�����������1����tanA=![]() =
=![]() ��tanB=
��tanB=![]() =
=![]()
��CE=![]() AE��CE=
AE��CE=![]() BE
BE
��![]() AE=
AE=![]() BE
BE
����AB=AE+BE=2
��AE=1.2
��CE=1.2��![]() =0.48��m��
=0.48��m��
��2������O��FG�Ĵ��ߣ�����ΪM������O��PQ�Ĵ��ߣ�����ΪN����
FM=1��MH=ON=1.2��1=0.2
��O��FG��PQ�ľ���֮��Ϊ5��2
��OM=0.5=NH
����OF��OP����
ֱ��������OFM�У�OF=![]() =OP
=OP
��ֱ��������OPN�У�PN=![]() =1.1
=1.1
��PH=PN��NH=1.1��0.5=0.6��m��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�г���շѷ�ʽ���£���ʻ������3 km����(����3 km)����5Ԫ������3 km��ÿ����ʻ1 km����2Ԫ����˳�����y(Ԫ)��˳�����x(km)(x��3)֮��ĺ�������ʽΪ____________(����Ҫд���Ա�����ȡֵ��Χ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
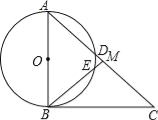
����Ŀ����ͼ����ֱ����ABC�У���ABC=90������M��AC���е㣬��ABΪֱ������O�ֱ�AC��BM�ڵ�D��E��
��1����֤��MD=ME��
��2����գ�����OE��OD������A�Ķ���Ϊ ʱ���ı���ODME�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
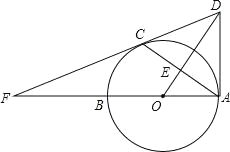
����Ŀ����ͼ����֪AB����O��ֱ����C����O�ϵĵ㣬��OE��AC�ڵ�E������C����O�����ߣ���OE���ӳ����ڵ�D����AB���ӳ����ڵ�F������AD����1����֤��AD����O�����ߣ�
��2����cos��BAC=![]() ��AC=8�����߶�AD�ij���
��AC=8�����߶�AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ�����1����2��0����3��������С��һ������ ��
A. 1 B. ��2 C. 0 D. ��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��4��3������y��ĶԳƵ����ڵ������ǣ�������
A.��һ����B.�ڶ�����C.��������D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2x��k��2��0����������ȵ�ʵ��������ʵ��k��ȡֵ��Χ��(�� ��)
A.k�ݣ�3B.k��3C.k����3D.k��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
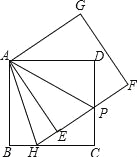
����Ŀ����ͼ���ڱ߳�Ϊ6��������ABCD�У���������ABCD�Ƶ�A��ʱ����ת�ǶȦ���0��������90�㣩���õ�������AEFG��EF���߶�CD�ڵ�P��FE���ӳ��߽��߶�BC�ڵ�H������AH��AP��
��1����֤����ADP�ա�AEP��
��2��������HAP�Ķ��������ж��߶�HP��BH��DP��������ϵ����˵�����ɣ�
��3������DE��EC��CF��DF�õ��ı���CFDE������ת�����У��ı���CFDE�ܷ�Ϊ���Σ����ܣ����BH��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com