
| d,a,r之间的关系 | ⊙O与正方形的公共点个数 |
| d>a+r | 0 |
| d=a+r | 1 |
| a-r<d<a+r | 2 |
| d=a-r | 1 |
| 0≤d<a-r | 0 |
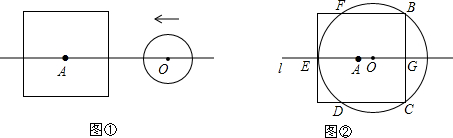
分析 (1)当r<a时,⊙A的直径小于正方形的边长,⊙A与正方形中垂直于直线l的一边相离、相切、相交,三种情况,故可确定⊙O与正方形的交点个数;
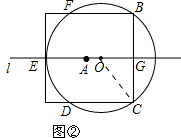
(2)如图②,当⊙O与正方形有5个公共点时,连接OC,用a、r表示△COG的各边长,在Rt△OCG中,由勾股定理求a、r的关系;
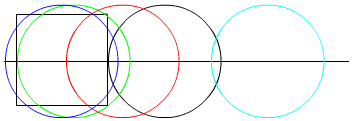
(3)当r=a时,⊙O的直径等于正方形的边长,此时会出现⊙A与正方形相离,与正方形一边相切,相交,与正方形四边相切,四种情况,故可确定⊙O与正方形的交点个数;
(4)当r与a之间满足(2)中的数量关系,即5a=4r,⊙O与正方形的公共点个数为5个.
解答 解:(1)如图①,
| d,a,r之间的关系 | ⊙O与正方形的公共点个数 |
| d>a+r | 0 |
| d=a+r | 1 |
| a-r<d<a+r | 2 |
| d=a-r | 1 |
| 0≤d<a-r | 0 |
| d、a、r之间关系 | 公共点的个数 |
| d>a+r | 0 |
| d=a+r | 1 |
| a≤d<a+r | 2 |
| d<a | 4 |
点评 本题是一道较为新颖的几何压轴题.考查圆、相似、正方形等几何知识,综合性较强,有一定的难度,试题的区分度把握非常得当,是一道很不错的压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
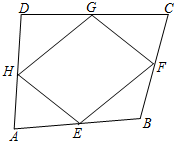 如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AC=BD.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AC=BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com