练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．若抛物线y=x2+mx+9与x轴相切，则此抛物线顶点的坐标是（3，0）或（-3，0），对称轴为x=3或x=-3．

    分析 首先根据抛物线y=x2+mx+9与x轴相切求出m的值，进而求出抛物线的顶点坐标以及对称轴．

    解答 解：∵抛物线y=x2+mx+9与x轴相切，
    ∴方程x2+mx+9=0有两个相等的根，
    ∴m2-4×9=0，
    ∴m=±6，
    则当m=-6时，y=（x-3）2，顶点坐标为（3，0），对称轴为x=3；
    当m=6时，y=（x+3）2，顶点坐标为（-3，0），对称轴为x=-3．
    故答案为（3，0）或（-3，0）；x=3或x=-3．

    点评 本题主要考查了二次函数的性质，解答本题的关键是根据题意得到抛物线顶点坐标在x轴上，此题难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    1．若2（x+4）-5＜3（x+1）+4的最小整数解是方程$\frac{1}{3}$x-mx=5的解，则m2-2m+11的平方根是$±\sqrt{11}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图所示，AC=DF，BD=EC，AC∥DF，∠ACB=80°，∠B=30°，则∠F=70°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若二次函数$y=m{x^2}+3x+\sqrt{3}$在平面直角坐标系中的图象与x轴有交点，则m的取值范围是（　　）
    A．m＞$\frac{{3\sqrt{3}}}{4}$B．m≤$\frac{{3\sqrt{3}}}{4}$且m≠0C．m＞$\frac{{\sqrt{3}}}{4}$D．m≤$\frac{{\sqrt{3}}}{4}$且m≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，△ABC≌△CDA，BD交AC于点O，则△ABC绕点O旋转180°后与△CDA重合，△ABO可以由△CDO绕点O旋转180°得到．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．抛物线y=x2-2x-1与坐标轴交点个数为（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷（解析版） 题型：解答题

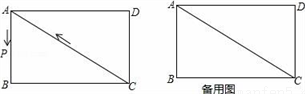
    如图，在长方形ABCD中，边AB、BC的长（AB＜BC）是方程x2﹣7x+12=0的两个根．点P从点A出发，以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动，运动时间为t（秒）．

    （1）求AB与BC的长；

    （2）当点P运动到边BC上时，试求出使AP长为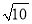时运动时间t的值；

    （3）当点P运动到边AC上时，是否存在点P，使△CDP是等腰三角形？若存在，请求出运动时间t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．在电影票上，将“3排6号”简记为（3，6），则（4，12）表示的意义是4排12号．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．求证：无论x取什么数，代数式3x2-6x+3.5的值永远为正数．

    查看答案和解析>>

    同步练习册答案