
分析 (1)根据题中所给的奇异三角形的定义容易得出结果;
(2)分c是斜边和b是斜边两种情况,再根据勾股定理判断出所给的三角形是否符合奇异三角形的定义;
(3)先根据勾股定理得出Rt△ABC各边之间的关系,再根据此三角形是奇异三角形可用a表示出b、c的值,即可得出结果.
解答 解:(1)设等边三角形的边长为a,
∵a2+a2=2a2,
∴等边三角形一定是奇异三角形,
∴“等边三角形一定是奇异三角形”,是真命题;
(2)①当c为斜边时,Rt△ABC不是奇异三角形;
②当b为斜边时,Rt△ABC是奇异三角形;理由如下:
分两种情况:
①当c为斜边时,b=$\sqrt{{c}^{2}-{a}^{2}}$=5$\sqrt{2}$,
∴a=b,
∴a2+c2≠2b2(或b2+c2≠2a2),
∴Rt△ABC不是奇异三角形.
②当b为斜边时,b=$\sqrt{{c}^{2}+{a}^{2}}$=5$\sqrt{6}$,
∵a2+b2=200
∴2c2=200
∴a2+b2=2c2
∴Rt△ABC是奇异三角形.
(3)在Rt△ABC中,a2+b2=c2,
∵c>b>a>0
∴2c2>a2+b2,2a2<b2+c2,
∵Rt△ABC是奇异三角形,
∴a2+c2=2b2,
∴2b2=a2+(a2+b2),
∴b2=2a2,
∴b=$\sqrt{2}$a
∵c2=a2+b2=3a2,
∴c=$\sqrt{3}$a
∴a:b:c=1:$\sqrt{2}$:$\sqrt{3}$.
点评 本题考查了奇异三角形的定义、等边三角形的性质、勾股定理;熟练掌握等边三角形的性质和勾股定理,在解答(2)时要注意分类讨论.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 学生 | 投进球数 | 没投进球数 | 投球次数 |
| 甲 | 10 | 5 | 15 |
| 乙 | a | b | 18 |
| A. | ①②③ | B. | ①③④ | C. | ①②③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
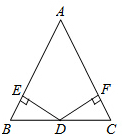 如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.
如图,在△ABC中,点D是边BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E、F,且DE=DF.试判断△ABC的形状,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1<k<2 | B. | -1<k<1 | C. | 1<k<2 | D. | 1<k<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com