
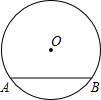
 如图,在⊙O中,已知半径为13,弦AB的长为24,那么圆心O到AB的距离为5.
如图,在⊙O中,已知半径为13,弦AB的长为24,那么圆心O到AB的距离为5.  星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:填空题
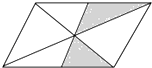 如图所示,平行四边形的两条对角线及过对角线交点的任意一条直线将平行四边形纸片分割成六个部分,现在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为$\frac{1}{4}$.
如图所示,平行四边形的两条对角线及过对角线交点的任意一条直线将平行四边形纸片分割成六个部分,现在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com