Question

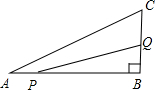
6．如图所示，在△ABC中，∠B=90°，AB=6cm，BC=3cm，点P以1cm/s的速度从点A开始沿边AB向点B移动，点Q以2cm/s的速度从点B开始沿边BC向点C移动，如果点P、Q分别从点A、B同时出发，（　　）s后P、Q之间的距离等于4$\sqrt{2}$cm．

• A． $\frac{2}{5}$
• B． 2
• C． $\frac{6}{5}$
• D． $\frac{2}{5}$或2

Answer 1

分析 设经过x秒，P、Q之间的距离等于4$\sqrt{2}$cm．先用含x的代数式分别表示BP和BQ的长度，进一步利用勾股定理建立方程求得答案即可．

解答 解：设点P、Q分别从点A、B同时出发，xs后P、Q之间的距离等于4$\sqrt{2}$cm，
∵AP=1•x=x，BQ=2x，
∴BP=AB-AP=6-x，
∴BP²+BQ²=PQ²，
即（6-x）²+（2x）²=（4$\sqrt{2}$）²，
解得：x₁=$\frac{2}{5}$，x₂=2（不合题意，舍去）．
答：点P、Q分别从点A、B同时出发，$\frac{2}{5}$s后P、Q之间的距离等于4$\sqrt{2}$cm．
故选：A．

点评 本题考查了一元二次方程的应用．关键是用含时间的代数式准确表示BP和BQ的长度，再根据勾股定理列出一元二次方程，进行求解．