
分析 分10是腰长和腰长的一半;15是腰长和腰长的一半两种情况讨论求解.
解答 解:∵等腰三角形一腰上的中线把三角形的周长分为10cm和15cm两部分,
∴若10cm是腰长和腰长的一半,
则腰长为10×$\frac{2}{3}$=$\frac{20}{3}$cm,
底边为15-$\frac{20}{3}$×$\frac{1}{2}$=$\frac{35}{3}$cm,
此时三角形的三边分别为$\frac{20}{3}$cm,$\frac{20}{3}$cm、$\frac{35}{3}$cm,能组成三角形;
若15是腰长和腰长的一半,
则腰长为15×$\frac{2}{3}$=10cm,
底边为10-10×$\frac{1}{2}$=5cm,
此时三角形的三边分别为10cm、10cm、5cm,能组成三角形;
综上所述,等腰三角形的腰长为$\frac{35}{3}$cm或5cm.
故答案为:$\frac{35}{3}$cm或5cm.
点评 本题考查了等腰三角形的性质,难点在于要分情况讨论并利用三角形的三边关系判断能组成三角形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
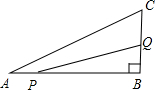 如图所示,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,( )s后P、Q之间的距离等于4$\sqrt{2}$cm.
如图所示,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,( )s后P、Q之间的距离等于4$\sqrt{2}$cm.| A. | $\frac{2}{5}$ | B. | 2 | C. | $\frac{6}{5}$ | D. | $\frac{2}{5}$或2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省长宁县双河学区八年级下学期第一次联考数学试卷(解析版) 题型:单选题
已知函数 y=(2m+1) x+m-3 ,若这个函数的图象不经过第二象限,则m的取值范围是( )
A. m>-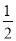 B. m<3 C.
B. m<3 C. 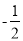 <m<3 D.
<m<3 D. 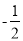 <m≤3
<m≤3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com