
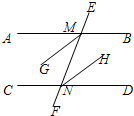
 如图,AB∥CD,MG平分∠AMN,NH平分∠MND.
如图,AB∥CD,MG平分∠AMN,NH平分∠MND.分析 (1)首先根据平行线的性质可得∠AMN=∠DNM,再根据角平分线的性质可得∠1=$\frac{1}{2}$,∠2=$\frac{1}{2}$,再根据等量代换可得∠1=∠2,最后根据内错角相等,两直线平行可得MG∥NH;
(2)根据(1)中的结论用语言叙述结论.
解答 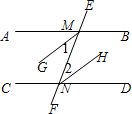 解:∵AB∥CD,
解:∵AB∥CD,
∴∠AMN=∠DNM (两直线平行,内错角相等),
∵MG平分∠AMN,NH平分∠MND,
∴∠1=$\frac{1}{2}∠$AMF,∠2=$\frac{1}{2}∠$DNE,
∴∠1=∠2),
∴MG∥NH;
(2)如果两直线平行,那么两内错角的平分线也互相平行.
点评 此题主要考查了平行线的判定与性质,角平分线的定义,关键证明∠1=∠2.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
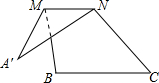 如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )| A. | 124° | B. | 92° | C. | 120° | D. | 116° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差值(单位:g) | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com