
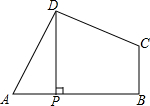
 如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长.
如图所示,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是36,求DP的长. 分析 作DE⊥BC,交BC延长线于E,如图,则四边形BEDP为矩形,再利用等角的余角相等得到∠ADP=∠CDE,则可利用“AAS”证明△ADP≌△CDE,得到DP=DE,S△ADP=S△CDE,所以四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,根据正方形的面积公式得到DP2=36,易得DP=6.
解答 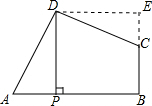 解:作DE⊥BC,交BC延长线于E,如图,
解:作DE⊥BC,交BC延长线于E,如图,
∵DP⊥AB,ABC=90°,
∴四边形BEDP为矩形,
∴∠PDE=90°,即∠CDE+∠PDC=90°,
∵∠ADC=90°,即∠ADP+∠PDC=90°,
∴∠ADP=∠CDE,
在△ADP和△CDE中,
$\left\{\begin{array}{l}{∠APD=∠CED}\\{∠ADP=∠CDE}\\{AD=DC}\end{array}\right.$,
∴△ADP≌△CDE,
∴DP=DE,S△ADP=S△CDE,
∴四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,
∴DP2=36,
∴DP=6.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了正方形的性质和勾股定理.本题的关键的作辅助线构造两个全等的三角形.


科目:初中数学 来源: 题型:选择题
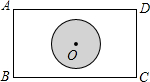 如图所示,一矩形公园中有一圆形湖,湖心O恰在矩形的中心位置,若测得AB=600m,BC=800m,则湖心O到四个顶点的距离为( )
如图所示,一矩形公园中有一圆形湖,湖心O恰在矩形的中心位置,若测得AB=600m,BC=800m,则湖心O到四个顶点的距离为( )| A. | 300m | B. | 400m | C. | 500m | D. | 600m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
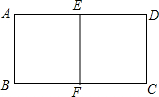 用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃,设AB边长为xm,花圃面积为Sm2.
用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃,设AB边长为xm,花圃面积为Sm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ | C. | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{2}$$÷\sqrt{3}$=$\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com