Question

4．在⊙O中，AB，CD为⊙O的弦，且AB∥CD，AB=24，CD=10，弦AB的弦心距为5，则AB和CD之间的距离是7或17．

Answer 1

分析 根据题意画出图形，由于AB、CD在圆心的同侧或异侧不能确定，故应分两种情况进行讨论．

解答 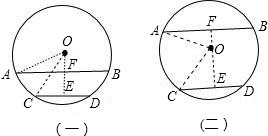解：①当AB、CD在圆心的同侧，如图（一）所示时，过O作OE⊥CD，交AB于F，连接OA、OC，
由垂径定理可知AF=$\frac{1}{2}$AB=$\frac{1}{2}$×24=12，CE=$\frac{1}{2}$CD=$\frac{1}{2}$×10=5，
在Rt△AOF中，OA=$\sqrt{A{F}^{2}+O{F}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13；
所以OC=13，
在Rt△ACOE中，OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12，
故EF=OE-OF=12-5=7；
②当AB、CD在圆心的异侧，如图（二）所示时，过O作OE⊥CD，交AB于F，连接OA、OC，
同（一）可知：OE=12，OF=5，EF=OE+OF=12+5=17；
故答案为：7或17．

点评 本题考查了勾股定理和垂径定理的应用．此题难度适中，解题的关键是注意掌握数形结合思想与分类讨论思想的应用，小心别漏解．