
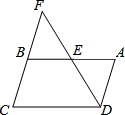
 如图,在平行四边形ABCD中,AB=8,AD=6,E是AB上一动点,AE=x,DE的延长线交CB的延长线于点F,设CF=y.
如图,在平行四边形ABCD中,AB=8,AD=6,E是AB上一动点,AE=x,DE的延长线交CB的延长线于点F,设CF=y.分析 (1)由平行四边形的性质,利用“角角”证明△ADE∽△CFD,根据相似三角形对应边的比相等,得出y与x之间的函数关系即可;
(2)由(1)的函数关系即可得到自变量x的取值范围.
解答 解:(1)∵四边形ABCD为平行四边形,
∴∠A=∠C,∠ADE=∠F,
∴△ADE∽△CFD
∴$\frac{AD}{CF}=\frac{AE}{CD}$,
∵AB=8,AD=6,
∴AB=CD=8,AD=BC=6,
∴$\frac{6}{y}=\frac{x}{8}$,
∴y=$\frac{48}{x}$;
(2)由(1)可知0<x<8.
点评 本题考查了平行四边形性质,相似三角形的性质和判定的应用,关键是证出△FEB∽△FDC.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
| A. | a是任意实数时,都有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | B. | 只有a是正数时,才有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | ||
| C. | 当a为有理数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | D. | 当a≥0时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
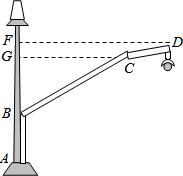 如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
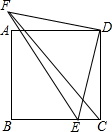 如图,在正方形ABCD中,E是BC上的动点(不与点B、C重合),连接DE,过点D作FD⊥ED于点D,并使FD=ED,连接CF,EF,下列角的大小比较中,一定正确的是( )
如图,在正方形ABCD中,E是BC上的动点(不与点B、C重合),连接DE,过点D作FD⊥ED于点D,并使FD=ED,连接CF,EF,下列角的大小比较中,一定正确的是( )| A. | ∠ADF>∠CDE | B. | ∠DCF>∠DFC | C. | ∠DFC>∠ADF | D. | ∠DEC>∠BEF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com