
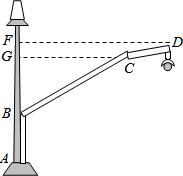
 如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36) 科目:初中数学 来源: 题型:选择题
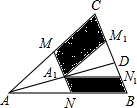 如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为( )
如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为( )| A. | 14 | B. | 21 | C. | 28 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
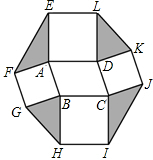 以?ABCD的四条边为边,在其形外分别作正方形,如图,连接EF、GH、IJ、KL.若?ABCD的面积为5,则图中阴影部分四个三角形的面积和为( )
以?ABCD的四条边为边,在其形外分别作正方形,如图,连接EF、GH、IJ、KL.若?ABCD的面积为5,则图中阴影部分四个三角形的面积和为( )| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
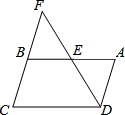 如图,在平行四边形ABCD中,AB=8,AD=6,E是AB上一动点,AE=x,DE的延长线交CB的延长线于点F,设CF=y.
如图,在平行四边形ABCD中,AB=8,AD=6,E是AB上一动点,AE=x,DE的延长线交CB的延长线于点F,设CF=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
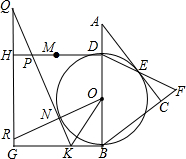 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,交BC的延长线于点F,CF=1,cos∠ABC=$\frac{3}{5}$.
如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,交BC的延长线于点F,CF=1,cos∠ABC=$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com