已知实数m.n满足m-n2=2.则代数式m2+2n2+4m-3的最小值等于( )A．9B．6C．-8D．-16 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

7．已知实数m，n满足m-n²=2，则代数式m²+2n²+4m-3的最小值等于（　　）

A．

B．

C．

-8

D．

-16

分析把m-n²=2变形为n²=m-2，代入所求式子，根据配方法进行变形，利用偶次方的非负性解答即可．

解答解：∵m-n²=2，
∴n²=m-2≥0，m≥2，
∴m²+2n²+4m-3
=m²+2m-4+4m-3
=m²+6m+9-16
=（m+3）²-16，
则代数式m²+2n²+4m-3的最小值等于（2+3）²-16=9．
故选：A．

点评此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

17．

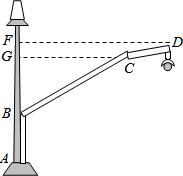如图，马路边安装的路灯由支柱上端的钢管ABCD支撑，AB=25cm，CG⊥AF，FD⊥AF，点G、点F分别是垂足，BG=40cm，GF=7cm，∠ABC=120°，∠BCD=160°，请计算钢管ABCD的长度．（钢管的直径忽略不计，结果精确到1cm．参考数据：sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

18．

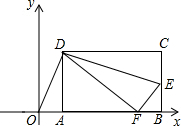如图，矩形ABCD的顶点AB在x轴上，点D的坐标为（6，8），点E在边BC上，△CDE沿DE翻折后点C恰好落在x轴上点F处，若△ODF为等腰三角形，点E的坐标为（16，3）或（4$\sqrt{5}$+6，2$\sqrt{5}$-2）或（$\frac{43}{3}$，$\frac{7}{4}$）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．计算：
（1）$\frac{m^2}{m-2}+\frac{4}{2-m}$
（2）$\frac{{x}^{2}-1}{{x}^{2}+2x}÷\frac{x-1}{x}$
（3）$\frac{x^2}{x-1}-x-1$
（4）$（\frac{1}{x-1}-\frac{1}{x+1}）÷\frac{x}{{2{x^2}-2}}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．计算：
（1）$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
（2）（1+$\sqrt{3}$）（1-$\sqrt{3}$）-（2$\sqrt{3}$-1）²．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

12．点A（3，-3）在第四象限；
点B（-3，2）在第二象限；
点C（-2，0）在x轴上；
点D（0，4）在y轴上．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

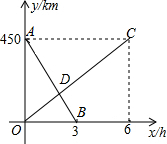一列快车由甲地开往乙地，一列慢车由乙地开往甲地，两车同时出发，匀速运动．快车离乙地的路程y₁（km）与行驶的时间x（h）之间的函数关系，如图中线段AB所示；慢车离乙地的路程y₂（km）与行驶的时间x（h）之间的函数关系，如图中线段0C所示．根据图象进行以下研究．
解读信息：
（1）甲、乙两地之间的距离为450km；
（2）快车的速度是150km/h，慢车的速度是75km/h．
（3）求线段AB与线段OC的解析式；
（4）快、慢两车在何时相遇？相遇时距离乙地多远？

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

16．