
���� ��1���Ķ����ϣ��������ֵ����������ֵ����Ĵ���ʽ����0�����ɽ��
��2�������Ķ������У����������ֵ�Ĵ���ʽ�ķ���������x��ȡֵ��Χ����Ϊ������������ݾ���ֵ�����ʽ�ɣ�
��3����ȵڣ�2��С��ķ�������Ϊ����������õ�����һԪһ�η��̣��ⷽ�̼��ɣ�
��� �⣺��1����x+2=0����x=-2����x-4=0����x=4��
����|x+2|��|x-4|�����ֵ�ֱ���-2��4��
��2���ٵ�x��-2ʱ��ԭʽ=-��x+2��-[-��x-4��]=-6��
�ڵ�-2��x��4ʱ��ԭʽ=��x+2��-[-��x-4��]=2x-2��
�۵�x��4ʱ��ԭʽ=��x+2��-��x-4��=6��
��3���ⷽ��|x-1|+|x+3|=6��
�ٵ�x��-3ʱ�����̿ɻ�Ϊ��-��x-1��-��x+3��=6����á�x=-4��
�ڵ�-3��x��1ʱ�����̿ɻ�Ϊ��-��x-1��+��x+3��=6����4=6�����Բ����ڷ���������x��
�۵�x��1ʱ�����̿ɻ�Ϊ����x-1��+��x+3��=6����á�x=2��
�������������̵Ľ���x=-4��x=2��
���� ������Ҫ�������ֵ��һԪһ�η��̣��������Ķ��͵���Ŀ����Ҫ�����Ķ����ϣ��������ֵ�����������ֵ�Ĵ���ʽ�ķ����ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B�� | $\sqrt{8}��\sqrt{2}=4$ | C�� | $2+\sqrt{3}=2\sqrt{3}$ | D�� | $\frac{{\sqrt{10}}}{2}=\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
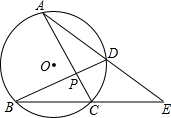 ��ͼ��AC��BD����P��AD��BC�ӳ����ڵ�E����AEC=37�㣬��CAE=31�㣬���APB�Ķ���Ϊ99�㣮
��ͼ��AC��BD����P��AD��BC�ӳ����ڵ�E����AEC=37�㣬��CAE=31�㣬���APB�Ķ���Ϊ99�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
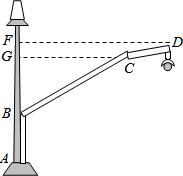 ��ͼ����·�߰�װ��·����֧���϶˵ĸֹ�ABCD֧�ţ�AB=25cm��CG��AF��FD��AF����G����F�ֱ��Ǵ��㣬BG=40cm��GF=7cm����ABC=120�㣬��BCD=160�㣬�����ֹ�ABCD�ij��ȣ����ֹܵ�ֱ�����Բ��ƣ������ȷ��1cm���ο����ݣ�sin10���0.17��cos10���0.98��tan10���0.18��sin20���0.34��cos20���0.94��tan20���0.36��
��ͼ����·�߰�װ��·����֧���϶˵ĸֹ�ABCD֧�ţ�AB=25cm��CG��AF��FD��AF����G����F�ֱ��Ǵ��㣬BG=40cm��GF=7cm����ABC=120�㣬��BCD=160�㣬�����ֹ�ABCD�ij��ȣ����ֹܵ�ֱ�����Բ��ƣ������ȷ��1cm���ο����ݣ�sin10���0.17��cos10���0.98��tan10���0.18��sin20���0.34��cos20���0.94��tan20���0.36���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
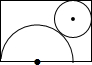 ��ͼ����һ�ž���Ӳֽ���м���һ����Բ�κ�һ��Բ�Σ�ʹ֮ǡ��Χ��һ��Բ�������Բ�IJ����S���͵����S���Ĺ�ϵ�ǣ�������
��ͼ����һ�ž���Ӳֽ���м���һ����Բ�κ�һ��Բ�Σ�ʹ֮ǡ��Χ��һ��Բ�������Բ�IJ����S���͵����S���Ĺ�ϵ�ǣ�������| A�� | S��=S�� | B�� | S��=2S�� | C�� | S��=3S�� | D�� | S��=4S�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com