练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知点P是线段AB的黄金分割点，若AB=2，则PB=$\sqrt{5}-1或3-\sqrt{5}$．

    分析 根据黄金分割点的定义，分AP＞BP和AP＜BP两种情况，AP=$\frac{\sqrt{5}-1}{2}$AB叫做黄金比进行计算，代入数据即可得出AP的长．

    解答 解：当AP＞BP时，
    AP=$\frac{\sqrt{5}-1}{2}$×2=$\sqrt{5}$-1，
    当AP＜BP时，
    AP=2-（$\sqrt{5}$-1）=3-$\sqrt{5}$．
    故答案为：$\sqrt{5}-1或3-\sqrt{5}$．

    点评 本题考查的是黄金分割的概念，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图1，已知AB⊥BM，AB=2，点P为射线BM上的动点，联结AP，作BH⊥AP，垂足为H，∠APM的平分线交BH的延长线于点D，联结AD．
    （1）若∠BAP=30°，求∠ADP的度数；
    （2）若S△ADP：S△ABP=3：2，求BP的长；
    （3）若AD∥BM（如图2），求BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．某地实现全年旅游综合收入908600000元，数908600000用科学记数法表示为9.086×108．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列命题中，正确的命题个数有（　　）
    ①平分一条弦的直径一定垂直于弦；
    ②相等的两个圆心角所对的两条弧相等；
    ③两个相似梯形的面积比是1：9，则它们的周长比是1：3；
    ④在⊙O中，弦AB把圆周分成1：5两部分，则弦AB所对的圆周角是30°；
    ⑤△ABC中，b=3，c=5，那么sinB=$\frac{3}{5}$；
    ⑥△ABC中，AD为BC边上的高，若AD=1，BD=1，CD=$\sqrt{3}$，则∠BAC的度数为105°．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．家住滨河国际一单元的甲、乙二人同时从地下车库进入电梯回家，已知两人到1至4层的任意一层出电梯，并设甲在a层出电梯，乙在b层出电梯．
    （1）用树状图或列表法表示（a，b）的所有可能结果，并求甲、乙二人在同一层楼出电梯的概率：
    （2）小亮和小芳打赌，若甲、乙住在同层，则小亮胜，否则小芳胜．判断上述游戏是否公平？若公平，请说明理由；若不公平，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

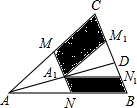    7．如图，M、N分别是△ABC的边AC和AB的中点，D为BC上任意一点，连接AD，将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上，已知△AMN的面积为7，则图中阴影部分的面积为（　　）
    A．14B．21C．28D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如果直线a、直线b都和直线c平行，那么直线a和直线b的位置关系是（　　）
    A．相交B．平行C．相交或平行D．不相交

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

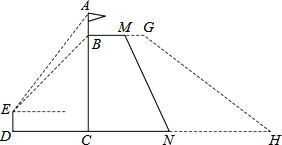    11．如图，我国某边防哨所树立了“祖国在我心中”建筑物，它的横截面为四边形BCNM，其中BC⊥CN，BM∥CN，建筑物顶上有一旗杆AB，士兵小明站在D处，由E点观察到旗杆顶部A的仰角为52°，底部B的仰角为45°，已知旗杆AB=2.8米，DE=1.8米．
    （参考数据：sin52°≈0.788，tan52°≈1.280）
    （1）求建筑物的高度BC；
    （2）建筑物长50米，背风坡MN的坡度i=1：0.5，为提高建筑物抗风能力，士兵们在背风坡填筑土石方加固，加固后建筑物顶部加宽4.2米，背风坡GH的坡度为i=1：1.5，施工10天后，边防居民为士兵支援的机械设备终于到达，这样工作效率提高到了原来的2倍，结果比原计划提前20天完成加固任务，士兵们原计划平均每天填筑土石方多少立方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．阅读下列材料并解决有关问题：
    我们知道|x|=$\left\{{\begin{array}{l}{x（x＞0）}\\{0（x=0）}\\{-x（x＜0）}\end{array}}\right.$，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x-2|时，可令x+1=0和x-2=0，分别求得x=-1，x=2（称-1，2分别为|x+1|与|x-2|的零点值）．在有理数范围内，零点值x=-1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况：（1）x＜-1；（2）-1≤x＜2；（3）x≥2．
    从而化简代数式|x+1|+|x-2|可分以下3种情况：
    （1）当x＜-1时，原式=-（x+1）-（x-2）=-2x+1；
    （2）当-1≤x＜2时，原式=x+1-（x-2）=3；
    （3）当x≥2时，原式=x+1+x-2=2x-1．
    通过以上阅读，请你解决以下问题：
    （1）分别求出|x+2|和|x-4|的零点值；
    （2）化简代数式|x+2|-|x-4|；
    （3）解方程|x-1|+|x+3|=6．

    查看答案和解析>>

    同步练习册答案