
分析 (1)根据题意和实际情况,可选用列表法求各自的概率.
(2)可以添加一定的分值进行调节.
解答 解:(1)列表如下:
| 甲 乙 | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,2) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:填空题
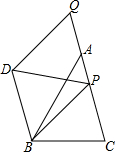 如图,在△ABC中,AB=6,tan∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为$\frac{18}{5}$.
如图,在△ABC中,AB=6,tan∠BAC=$\frac{3}{4}$,点P为AC边上任意一点,点Q为CA延长线上任意一点,以PB、PQ为两边作?PQDB,则对角线PD的最小值为$\frac{18}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
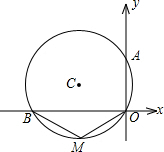 如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°.
如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com