
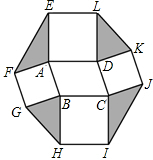
 以?ABCD的四条边为边,在其形外分别作正方形,如图,连接EF、GH、IJ、KL.若?ABCD的面积为5,则图中阴影部分四个三角形的面积和为( )
以?ABCD的四条边为边,在其形外分别作正方形,如图,连接EF、GH、IJ、KL.若?ABCD的面积为5,则图中阴影部分四个三角形的面积和为( )| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
分析 过D作DN⊥AB于N,过E作EM⊥FA交FA延长线于M,连接AC,BD,求出∠EAM=∠BAD,根据锐角三角形函数定义求出EM=DN,求出△AEF和△ABD面积相等,同理求出S△BHG=S△ABC,S△CIJ=S△CBD,S△DLK=S△DAC,代入S=S△AEF+S△BGH+S△CIJ+S△DLK得出S=2S平行四边形ABCD,代入求出即可.
解答  解:过D作DN⊥AB于N,过E作EM⊥FA交FA延长线于M,连接AC,BD,
解:过D作DN⊥AB于N,过E作EM⊥FA交FA延长线于M,连接AC,BD,
∵四边形ABGF和四边形ADLE是正方形,
∴AE=AD,AF=AB,∠FAB=∠EAD=90°,
∴∠EAF+∠BAD=360°-90°-90°=180°,
∵∠EAF+∠EAM=180°,
∴∠EAM=∠DAN,
∴sin∠EAM=$\frac{EM}{AE}$,sin∠DAN=$\frac{DN}{AD}$,
∵AE=AD,
∴EM=DN(也可以证明△EAM≌△DAN得到),
∵S△AEF=$\frac{1}{2}$AF×EM,S△ADB=$\frac{1}{2}$AB×DN,
∴S△AEF=S△ABD,
同理S△BHG=S△ABC,S△CIJ=S△CBD,S△DLK=S△DAC,
∴阴影部分的面积S=S△AEF+S△BGH+S△CIJ+S△DLK=2S平行四边形ABCD=2×5=10.
故选B.
点评 本题考查了平行四边形的性质,锐角三角函数的定义,三角形的面积等知识点的应用,主要考查学生运用定理进行推理和计算的能力,题目比较好,但有一定的难度.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{8}×\sqrt{2}=4$ | C. | $2+\sqrt{3}=2\sqrt{3}$ | D. | $\frac{{\sqrt{10}}}{2}=\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a是任意实数时,都有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | B. | 只有a是正数时,才有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | ||
| C. | 当a为有理数时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立 | D. | 当a≥0时,有($\sqrt{a}$)2=$\sqrt{a^2}$成立 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
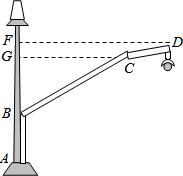 如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
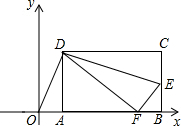 如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(6,8),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点E的坐标为(16,3)或(4$\sqrt{5}$+6,2$\sqrt{5}$-2)或($\frac{43}{3}$,$\frac{7}{4}$).
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(6,8),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点E的坐标为(16,3)或(4$\sqrt{5}$+6,2$\sqrt{5}$-2)或($\frac{43}{3}$,$\frac{7}{4}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com