
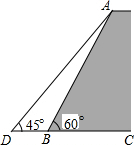
 如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米?(结果保留到0.1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米?(结果保留到0.1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 过A点作AE⊥CD于E,在Rt△ABE中,根据∠ABE=60°,AB=30m,求出AE的长度,然后再Rt△ADE中求出DE的长度,继而可求得BD的长度.
解答 解:过A点作AE⊥CD于E.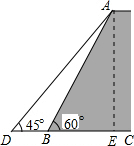
在Rt△ABE中,
∵∠ABE=60°.
∴AE=AB•sin60°=30×$\frac{\sqrt{3}}{2}$=15$\sqrt{3}$(米),
BE=AB•cos60°=30×$\frac{1}{2}$=15(米),
在Rt△ADE中,
∵∠ADB=45°,
∴DE=AE=15$\sqrt{3}$(米),
∴DB=DE-BE=15$\sqrt{3}$-15≈11.0(米).
故此时应将坝底向外拓宽大约11.0米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据题目所给的坡角构造直角三角形,利用三角函数的知识求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | m<n | B. | m=n | C. | m>n | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com