
【题目】如图,已知数轴上点A表示的数为8,A是数轴上位于点B右侧的一点,且AB=26动点P从A点出发,每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>s)秒.
![]()
(1)数轴上点B表示的数______点P表示的数______(用含 t 的代数式表示)
(2)若M为AP的中点N为BP的中点,在点P运动的过程中,线段MN的长度是______.
(3)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?
(4)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
【答案】(1)-18,8-5t;(2)13;(3)![]() 秒或4秒时P、Q之间的距离恰好等于2;(4)点P运动13秒时追上点Q.
秒或4秒时P、Q之间的距离恰好等于2;(4)点P运动13秒时追上点Q.
【解析】
(1)根据数轴上的点表示的数右边总比左边的数大及数轴上两点间的距离公式即可得点B表示的数及点P表示的数;(2)分点P在点B左边和右边两种情况,利用数轴上两点间的距离公式可求出BP、AP的长,根据中点的定义可得出PM、PN的长,即可求出MN的长;(3)利用两点间距离公式求出PQ的长即可;(4)分别求出点P、点Q表示的数,根据追上时P、Q表示的数相同即可得答案.
(1)∵A是数轴上位于点B右侧的一点,且AB=26,
∴点B表示的数为8-26=-18,
∵点P从A向左运动,速度为每秒5个单位长度,
∴点P表示的数为:8-5t,
故答案为:-18,8-5t
(2)①如图,当点P在点B右边时,
∵AP=5t,
∴BP=26-5t,
∵M、N分别为AP、BP的中点,
∴PM=![]() t,PN=
t,PN=![]() =13-
=13-![]() t,
t,
∴MN=PM+PN=![]() t+13-
t+13-![]() t=13,
t=13,
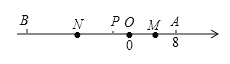
②如图,当点P在点B左边时,
∵AP=5t,
∴BP=5t-26,
∵M、N分别为AP、BP的中点,
∴PM=![]() t,PN=
t,PN=![]() =
=![]() t-13,
t-13,
∴MN=PM-PN=![]() t-(
t-(![]() t-13)=13,
t-13)=13,
![]()
综上所述:MN的长为13.
故答案为:13
(3)∵点P从A向左运动,速度为每秒5个单位长度,点Q从B向右运动,速度为2个单位长度,
∴点P表示的数为8-5t,点Q表示的数为-18+2t,
∴PQ=![]() =2,即
=2,即![]() =2,
=2,
∴26-7t=2或26-7t=-2,
解得:t=![]() 或t=4,
或t=4,
∴![]() 秒或4秒时P、Q之间的距离恰好等于2.
秒或4秒时P、Q之间的距离恰好等于2.
(4)∵P、Q都向左运动,速度分别为每秒5个单位长度和3个单位长度,
∴点P表示的数为8-5t,点Q表示的数为-18-3t,
∵点P追上点Q时,P、Q表示的数相同,
∴8-5t=-18-3t,
解得:t=13.
答:点P运动13秒时追上点Q.


科目:初中数学 来源: 题型:
【题目】据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题.
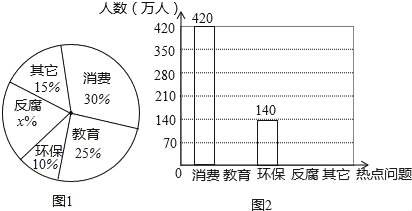
(1)求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)为了深度了解成都网民对政府工作报告的想法,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表.请你用列表法或画树状图的方法,求出一次所选代表恰好是丙和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
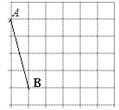
【题目】如图网格中每个小正方形的边长均为1,线段AB、CD的端点都在小正方形的顶点上.
(1)图(1)中,画一个以线段AB一边的四边形ABEF,且四边形ABEF是面积为7的中心对称图形,点E、F都在小正方形的顶点上,并直接写出线段BE的长;
(2)在图(2)中,画一个以线段CD为斜边直角三角形CDG,且△CDG的面积是2,点G在小方形的顶点上。
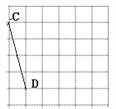
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司改革实行每月考核再奖励的新制度,大大调动了员工的积极性,2019年王明在公司前七个月每月奖金的变化如下表;(正数表示比前一月多的钱数,负数表示比前一 月少的钱数,单位;元)

设王明2018年12月份奖金为a元.
(1)用含a的代数式表示2019年四月份的奖金;
(2)请直接写出2019年一月到七月中王明得到奖金最多是哪个月?最少是哪个月?他们相差多少元?
(3)若2019年前七个月,王明得到奖金最多的那个月的奖金是2800元,请求出a的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
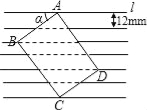
【题目】如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图. 根据上述信息,解答下列问题:

(1)本次抽取的学生人数是 ______ ;扇形统计图中的圆心角α等于 ______ ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月区教育局在全区中小学开展了“情系新疆书香援疆”捐书活动.某学校学生社团对部分学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:
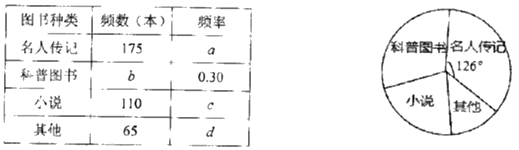
(1)统计表中的![]() _____________,
_____________,![]() _____________,
_____________,![]() _____________,
_____________,![]() _____________;
_____________;
(2)科普图书在扇形统计图中的圆心角是_____________°;
(3)若该校共捐书1500本,请估算“科普图书”和“小说”一共多少本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com