
����Ŀ��2019��5������������ȫ����Сѧ��չ�ˡ���ϵ�½�����Ԯ����������ijѧУѧ�����ŶԲ���ѧ������ͼ�����ͳ�ƣ������ռ������ݻ��������治������ͳ��ͼ�����������ͳ��ͼ�������ṩ����Ϣ����������⣺
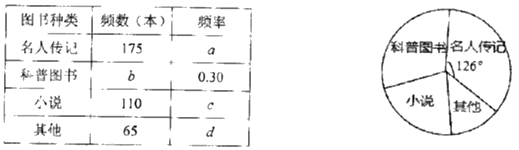
��1��ͳ�Ʊ��е�![]() _____________��
_____________��![]() _____________��
_____________��![]() _____________��
_____________��![]() _____________��
_____________��
��2������ͼ��������ͳ��ͼ�е�Բ�Ľ���_____________�㣻
��3������У������1500��������㡰����ͼ�顱�͡�С˵��һ�����ٱ���

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P��Q�Ƿ���ֽ�е�����㣬�밴Ҫ����PQΪ�Խ��ߵĸ���ı���.�����㶼�ڸ���ϵ��ı��γ�Ϊ����ı��Σ�
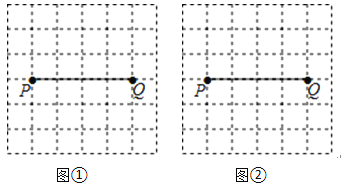
��1����ͼ���л���һ�������С�����ĶԳ�ͼ��PAQB��
��2����ͼ���л���һ���ı���PCQD��ʹ������Գ�ͼ�ε��������ĶԳ�ͼ�Σ�����һ���Խ���CD���߶�PQ��ijһ���Ϊ��ת������ת�õ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�У���ABC��90����AB��1��BC��2�����߶�BC�Ƶ�C˳ʱ��ת90���õ��߶�CD������AD.

(1)˵����ACD����״���������ACD�����;
(2)�ѵ���ֱ�����ǰ尴��ͼ2�ķ�ʽ�ڷţ�����E��CB���ϣ�����F��DC���ӳ����ϣ�ֱ�Ƕ������C�غ�.��A��B��������ѡһ������
A .��ͼ3������DE��BF,
�����벢֤��DE��BF֮��Ĺ�ϵ���������ǰ��Ƶ�C��ʱ����ת��(0��������90��)��ֱ��д��DE��BF֮��Ĺ�ϵ.
B .��ͼ2�е����ǰ��Ƶ�C��ʱ����ת��(0������360��)����ͼ4��ʾ������BE��DF�����ӵ�C��BE���е�M,
�����벢֤��CM��DF֮��Ĺ�ϵ������CE��1��CM��![]() ʱ����ֱ��д������ֵ.
ʱ����ֱ��д������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ8��A��������λ�ڵ�B�Ҳ��һ�㣬��AB=26����P��A�������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t>s����.
![]()
(1)�����ϵ�B��ʾ����______��P��ʾ����______(�ú� t �Ĵ���ʽ��ʾ)
(2)��MΪAP���е�NΪBP���е㣬�ڵ�P�˶��Ĺ����У��߶�MN�ij�����______.
(3)����Q�ӵ�B����,��ÿ��2����λ���ȵ��ٶ����������������˶�,����P��Qͬʱ�������ʶ�����ʱP��Q֮��ľ���ǡ�õ���2?
(4)����Q�ӵ�B����,��ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʵ�P�˶�������ʱ�ϵ�Q?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��y=![]() x-4�ֱ���x�ᣬy�ύ��A��B���㣬��ֱ��l2���ڵ�C��-2��m������D��ֱ��l2��y��Ľ��㣬����A����ƽ��3����λ��������ƽ��8����λǡ�������D�غϣ�
x-4�ֱ���x�ᣬy�ύ��A��B���㣬��ֱ��l2���ڵ�C��-2��m������D��ֱ��l2��y��Ľ��㣬����A����ƽ��3����λ��������ƽ��8����λǡ�������D�غϣ�
��1����ֱ��l2�Ľ���ʽ��
��2����֪��E��n��-2����ֱ��l1��һ�㣬��ֱ��l2��x������ƽ�ƣ���ƽ�ƹ����У���ֱ��l2���߶�BE�н���ʱ����ƽ�ƾ���d��ȡֵ��Χ��
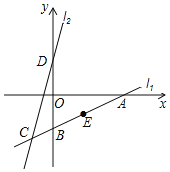
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɳ��ijѧУ�����꼶���ְ༶�����ǻۿ����Ե㣬һ����������ѧ�����ҳ�������ѧУ���������ڸ���༶�����ƹ㣬���ǵ�ƽ�������ʧ�������ѧУ�����ɹ�![]() ̨ƽ����Ժ�һ��ƽ���(ƽ���֧������
̨ƽ����Ժ�һ��ƽ���(ƽ���֧������![]() ֧).�ִ�
֧).�ִ�![]() ��
��![]() ���ҹ�˾�˽��ƽ����Լ۸���ÿ̨
���ҹ�˾�˽��ƽ����Լ۸���ÿ̨![]() Ԫ��ƽ���ÿ֧
Ԫ��ƽ���ÿ֧![]() Ԫ.
Ԫ.![]() ��˾���Ż�����Ϊÿ̨ƽ���������
��˾���Ż�����Ϊÿ̨ƽ���������![]() ֧ƽ��ʣ�
֧ƽ��ʣ�![]() ��˾���Ż�����Ϊ������Ŀ�������.
��˾���Ż�����Ϊ������Ŀ�������.
(1)����ѧУ��Ҫ����ƽ���![]() ֧���ú�
֧���ú�![]() �Ĵ���ʽ�ֱ��ʾ���ҹ�˾���ܷ���
�Ĵ���ʽ�ֱ��ʾ���ҹ�˾���ܷ���![]() ��
��![]() ��
��
(2)��ѧУȷ������![]() ̨ƽ����Ժ�
̨ƽ����Ժ�![]() ֧ƽ��������ҹ�˾��������ѡ������Ϊ������Ҫ���Ѷ��٣��������˵��.
֧ƽ��������ҹ�˾��������ѡ������Ϊ������Ҫ���Ѷ��٣��������˵��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ӿ����ͨƱ��20Ԫ/�������Ϊ�˴��������Ƴ������Żݿ���
�����ۼ�600Ԫ/����ÿ��ƾ�������շ���
�������ۼ�150Ԫ/����ÿ��ƾ������10Ԫ��
�����ͨƱ���������������Żݿ��������ʹ����������������Ӿx��ʱ�������ܷ���ΪyԪ��

��1���ֱ�д��ѡ����������ͨƱ����ʱ��y��x֮��ĺ�����ϵʽ��
��2����ͬһ����ϵ�������������ѷ�ʽ��Ӧ�ĺ���ͼ����ͼ��ʾ���������A��B��C��������
��3������ݺ���ͼ����ֱ��д��ѡ���������ѷ�ʽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
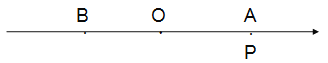
��1��д�������ϵ�B��ʾ���� _______����P��ʾ����________���ú�t�Ĵ���ʽ��ʾ����
��2������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʵ�P�˶�������ʱ�ϵ�Q����5�֣�
��3����MΪAP���е㣬NΪPB���е㣮��P���˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij�����5�֣�
��4������D��������һ�㣬��D��ʾ������x������̽��ʽ��|x+6|+|x-8|�Ƿ�����Сֵ������У�ֱ��д����Сֵ�����û�У�˵�����ɣ���5�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���������ABC�У�AB=AC���Եױ�BC�Ĵ�ֱƽ���ߺ�BC���ڵ�ֱ�߽���ƽ��ֱ������ϵ��������y=��![]() x2+
x2+![]() x+4����A��B���㣮
x+4����A��B���㣮

��1��д����A����B�����ꣻ
��2����һ����y���غϵ�ֱ��l��ÿ��2����λ���ȵ��ٶ�����ƽ�ƣ��ֱ��߶�OA��CA���������ڵ�E��M�͵�P������PA��PB����ֱ��l�ƶ���ʱ��Ϊt��0��t��4���룬���ı���PBCA�����S�������λ����t���룩�ĺ�����ϵʽ��������ı���PBCA����������
��3���ڣ�2���������£��Ƿ����t��ʹ�á�PAM��ֱ�������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com