练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，AM是△ABC的中线，D是线段AM的中点，AM＝AC，AE∥BC．求证：四边形EBCA是等腰梯形．

    【答案】见解析.

    【解析】

    根据三角形判定定理先证明三角形ADE与三角形MDC全等，得出AE=MC=MB，得出四边形AEBM是平行四边形，最后可证明四边形EBCA是等腰梯形．

    证明：∵AE∥BC，

    ∴∠AED＝∠MCD，

    ∵D是线段AM的中点，

    ∴AD＝MD，

    在△ADE和△MDC中，，

    ∴△ADE≌△MDC（AAS），

    ∴AE＝MC，

    ∵AM是△ABC的中线，

    ∴MB＝MC，

    ∴AE＝MB，

    ∵AE∥MB，

    ∴四边形AEBM是平行四边形，

    ∴BE＝AM，

    ∵AM＝AC，

    ∴BE＝AC，

    ∵AE∥BC，BE与AC不平行，

    ∴四边形EBCA是梯形，

    ∴梯形EBCA是等腰梯形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上点A表示的数为8，A是数轴上位于点B右侧的一点，且AB=26动点P从A点出发，每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t>s）秒.

    (1)数轴上点B表示的数______点P表示的数______(用含 t 的代数式表示)

    (2)若M为AP的中点N为BP的中点，在点P运动的过程中，线段MN的长度是______.

    (3)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2?

    (4)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】

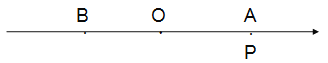
    （1）写出数轴上点B表示的数 _______，点P表示的数________（用含t的代数式表示）；

    （2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？（5分）

    （3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；（5分）

    （4）若点D是数轴上一点，点D表示的数是x，请你探索式子|x+6|+|x-8|是否有最小值？如果有，直接写出最小值；如果没有，说明理由．（5分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏西15°的方向．

    （1）∠AON＝　 　°；∠AOE＝　 　°；

    （2）求∠WOB的补角及∠AOB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上的A1，A2，A3，A4，……A20，这20个点所表示的数分别是a1，a2，a3，a4，……a20．若A1A2＝A2A3＝……＝A19A20，且a3＝20，|a1﹣a4|＝12．

    （1）线段A3A4的长度＝　 　；a2＝　 　；

    （2）若|a1﹣x|＝a2+a4，求x的值；

    （3）线段MN从O点出发向右运动，当线段MN与线段A1A20开始有重叠部分到完全没有重叠部分经历了9秒．若线段MN＝5，求线段MN的运动速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，梯形ABCD中，AB∥CD，BC⊥AB，AB＝AD，连接BD（如图a），点P沿梯形的边，从点A→B→C→D→A移动，设点P移动的距离为x，BP＝y．

    （1）求证：∠A＝2∠CBD；

    （2）当点P从点A移动到点C时，y与x的函数关系如图（b）中的折线MNQ所示，试求CD的长．

    （3）在（2）的情况下，点P从A→B→C→D→A移动的过程中，△BDP是否可能为等腰三角形？若能，请求出所有能使△BDP为等腰三角形的x的取值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=﹣x2+x+4经过A、B两点．

    （1）写出点A、点B的坐标；

    （2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；

    （3）在（2）的条件下，是否存在t，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知代数式是关于的二次多项式.

    （1）若关于的方程的解是，求的值；

    （2）若当时，代数式的值为-39，求当时，代数式的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上点表示数，点表示数，表示点和点之间的距离，且，满足.

    （1）求，两点之间的距离；

    （2）若在数轴上存在一点，且，直接写出点表示的数；

    （3）若在原点处放一挡板，一小球甲从点处以1个单位/秒的速度向左运动；同时另一小球乙从点处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为t（秒），
    ①分别表示甲、乙两小球到原点的距离（用t表示）；
    ②求甲、乙两小球到原点的距离相等时经历的时间.

    查看答案和解析>>

    同步练习册答案