
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:(1)∵F是AD的中点,
∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=![]() ∠BCD,故正确;
∠BCD,故正确;
(2)延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中, ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故正确;
(3)∵EF=FM,
∴S△EFC=S△CFM ,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
(4)设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°﹣x,
∴∠EFC=180°﹣2x,
∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x,
∵∠AEF=90°﹣x,
∴∠DFE=3∠AEF,故正确,
故选:C.
利用平行四边形的性质:平行四边形的对边相等且平行,再由全等三角形的判定得出△AEF≌△DMF(ASA),利用全等三角形的性质得出对应线段之间关系进而得出答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.
(1)求证:四边形MFNH为平行四边形;
(2)求证:△AMH≌△CNF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列关于a的单项式,探究其规律:a,3a2,5a3,7a4,9a5,….按照上述规律,第2019个单项式是( )
A. 2019a2019B. 4039a2019C. 4038a2019D. 4037a2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)试判断△BEC是否为等腰三角形,请说明理由?
(2)若AB=1,∠ABE=45°,求BC的长;
(3)在原图中画△FCE,使它与△BEC关于CE的中点O成中心对称,此时四边形BCFE是什么特殊平行四边形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
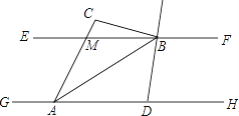
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 恩施州水资源丰富,全州水能资源理论存储量为509万千瓦,可开发量349.1万千瓦,将数509万用科学记数法表示为( )
A.0.509×107B.5.09×106C.5.09×105D.5.09×102
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com