
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,第一颗弹珠弹出后其速度![]() (米/分钟)与时间
(米/分钟)与时间![]() (分钟)前2分钟满足二次函数
(分钟)前2分钟满足二次函数![]() ,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.
,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.
(1)求第一颗弹珠的速度![]() (米/分钟)与时间
(米/分钟)与时间![]() (分钟)之间的函数关系式;
(分钟)之间的函数关系式;
(2)第一颗弹珠弹出1分钟后,弹出第二颗弹珠,第二颗弹珠的运行情况与第一颗相同,直接写出第二颗弹珠的速度![]() (米/分钟)与弹出第一颗弹珠后的时间
(米/分钟)与弹出第一颗弹珠后的时间![]() (分钟)之间的函数关系式;
(分钟)之间的函数关系式;
(3)当两颗弹珠同时在轨道上时,第____分钟末两颗弹珠的速度相差最大,最大相差______;
(4)判断当两颗弹珠同时在轨道上时,是否存在某时刻速度相同?请说明理由,并指出可以通过解哪个方程求出这一时刻.

【答案】(1)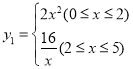 ;(2)
;(2)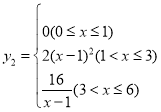 ;(3)第2分钟末两颗弹珠速度相差最大,最大相差6米/分钟;(4)存在,理由详见解析
;(3)第2分钟末两颗弹珠速度相差最大,最大相差6米/分钟;(4)存在,理由详见解析
【解析】
(1)将(1,2)代入![]() ,得
,得![]() ,从而得到
,从而得到![]() ,再代入
,再代入![]() 求出
求出![]() ,即可得到反比例函数解析式,即可得解;
,即可得到反比例函数解析式,即可得解;
(2)当![]() 时,第二颗弹珠未弹出,故第二颗弹珠的解析式为
时,第二颗弹珠未弹出,故第二颗弹珠的解析式为![]() ;再分别根据(1)中的结论,即可求出当
;再分别根据(1)中的结论,即可求出当![]() 和
和![]() 时第二颗弹珠的解析式;
时第二颗弹珠的解析式;
(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,则第2分钟末两颗弹珠速度相差最大,分别求出第2分钟末时两颗弹珠的速度,再相减即可的解;
(4)第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到5![]() 米/分钟,第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同.可以根据速度相等时列方程求得时刻.
米/分钟,第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同.可以根据速度相等时列方程求得时刻.
(1)当![]() 时,将(1,2)代入
时,将(1,2)代入![]() ,得
,得![]() ,
,
![]() ,
,
∵当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() ,
,
![]() 与
与![]() 的函数关系式为
的函数关系式为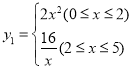 ;
;
(2)当![]() 时,第二颗弹珠未弹出,
时,第二颗弹珠未弹出,
∴第二颗弹珠的解析式为![]() ;
;
当![]() 时,第二颗弹珠的解析式为
时,第二颗弹珠的解析式为![]() ;
;
当![]() 时,第二颗弹珠的解析式为
时,第二颗弹珠的解析式为![]() ;
;
∴![]() 与
与![]() 的函数关系式为
的函数关系式为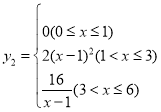 ;
;
(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,
∴第2分钟末两颗弹珠速度相差最大,
∵第一颗弹珠的速度为![]() 米/分钟,
米/分钟,
第二颗弹珠的速度为![]() 米/分钟,
米/分钟,
∴两颗弹珠的速度最大相差8-2=6米/分钟;
(4)存在,理由如下:
第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到5![]() 米/分钟,
米/分钟,
第二颗弹珠的速度由2米/分逐步上升到8米/分,
故在此期间必定存在一时刻,两颗弹珠的速度相同.
这个时刻可以通过解方程![]() 求得.
求得.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,B是边AD上一点,以AB为直径的
,B是边AD上一点,以AB为直径的![]() 经过点P,C是
经过点P,C是![]() 上一动点,连接AC,PC,PC交AB于点E,且
上一动点,连接AC,PC,PC交AB于点E,且![]() .
.
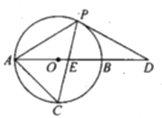
(1)求证:PD是![]() 的切线;
的切线;
(2)连接OP,PB,BC,OC,若![]() 的直径是4,则:
的直径是4,则:
①当四边形APBC是矩形时,求DE的长;
②当![]() ______时,四边形OPBC是菱形.
______时,四边形OPBC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
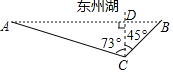
【题目】某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西两端之间AB的长.(结果精确到1米)(参考数据:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,![]() ≈1.414.)
≈1.414.)
查看答案和解析>>
科目:初中数学 来源: 题型:
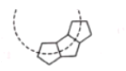
【题目】如图,若干同样的正五边形排成环状,图中所示的前3个正五边形,要完成这一圆环还需_____个正五边形,若将同样的正六边形排成环状,则需____个正六边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/千米 | 0.3元/分 | 0.8元/千米 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出部分每千米收0.8元. | |||
(1)小王与小张各自乘坐滴滴快车,在同一地点约见,已知到达约见地点,他们的实际行车里程分别为6千米与8.5千米,两人付给滴滴快车的乘车费相同(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算两人各自的实际乘车时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 在
在![]() 的左侧),交
的左侧),交![]() 轴于点
轴于点![]() ,且
,且![]() ,
,![]() .
.
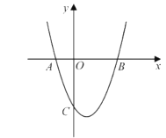
(1)求抛物线的解析式;
(2)点![]() 为第四象限抛物线上一点,过点
为第四象限抛物线上一点,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数关系式.(不要求写出
的函数关系式.(不要求写出![]() 的取值范围)
的取值范围)
(3)在(2)的条件下,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
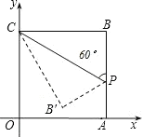
【题目】如图在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点p为边AB上的一点,![]() CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com