
【题目】如图,FE⊥AB于点E,AC⊥BF于点C,连结AF,EC,点M,N分别为AF,EC的中点,连结ME,MC. 
(1)求证:ME=MC.
(2)连结MN,若MN=8,EC=12,求AF的长.
【答案】
(1)证明:∵FE⊥AB,
∴∠AEF=90°,
∵M为AF中点,
∴EM= ![]() AF,
AF,
∵AC⊥BF,
∴∠ACF=90°,
∴CM= ![]() AF,
AF,
∴EM=CM
(2)解:∵N为EC中点,EM=CM,
∴MN⊥EC,CN= ![]() EC,
EC,
∵EC=12,
∴CN=6,
∵MN=8,
∴MC= ![]() =10,
=10,
∴AF=20.
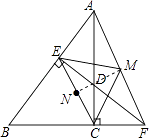
【解析】(1)首先根据FE⊥AB于点E,AC⊥BF于点C可得△AEF和△ACF是直角三角形,再根据在直角三角形中,斜边上的中线等于斜边的一半可得结论;(2)首先连接MN,根据等腰三角形的性质可得MN⊥EC,再利用勾股定理计算出MC的长,然后再计算AF长即可.
【考点精析】本题主要考查了直角三角形斜边上的中线的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边 PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论: 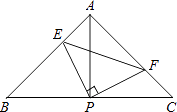
(1.)AE=CF;
(2.)△EPF是等腰直角三角形;
(3.)S四边形AEPF= ![]() S△ABC;
S△ABC;
(4.)EF=AP.
上述结论中始终正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果规定收入为正,支出为负,收入200元记作+200元,那么支出37元记作( )
A. 200元 B. -37元 C. 163元 D. 37元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据广东省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜游客约27700000人,将27700000用科学记数法表示为( )
A.0.277×107
B.0.277×108
C.2.77×107
D.2.77×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2 , 长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由. 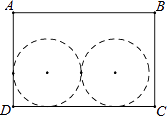
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com