
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边 PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论: 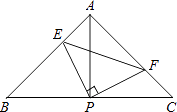
(1.)AE=CF;
(2.)△EPF是等腰直角三角形;
(3.)S四边形AEPF= ![]() S△ABC;
S△ABC;
(4.)EF=AP.
上述结论中始终正确的结论有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵△ABC中,AB=AC,∠BAC=90°,P是BC中点, ∴∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,
∴∠EPF﹣∠APF=∠APC﹣∠APF,
∴∠APE=∠CPF,
在△APE和△CPF中 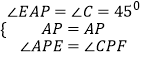 ,
,
∴△APE≌△CPF(ASA),
∴AE=CF,EP=PF,
∴△EPF是等腰直角三角形,∴①正确;②正确;
∵△APE≌△CPF
∴SAPE=S△CPF ,
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△APF=S△APC= ![]() S△ABC , ∴③正确;
S△ABC , ∴③正确;
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP= ![]() BC,
BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故④错误;
即正确的有3个,
故选C.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是( )
A.y=(x﹣1)2+2
B.y=(x+1)2+2
C.y=x2+1
D.y=x2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列四个命题:①两组邻边相等的四边形是平行四边形;②有三个角是直角的四边形是平行四边形;③有三个角相等的四边形是平行四边形;④一条对角线是另一条对角线的垂直平分线的四边形是平行四边形.其中真命题的个数是( )
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
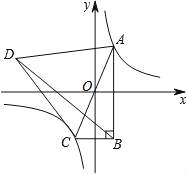
【题目】如图,已知双曲线y=![]() (k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20
(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20![]() ,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,FE⊥AB于点E,AC⊥BF于点C,连结AF,EC,点M,N分别为AF,EC的中点,连结ME,MC. 
(1)求证:ME=MC.
(2)连结MN,若MN=8,EC=12,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com