
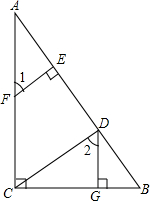
 如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,将下列证明EF∥CD的过程及理由填写完整.
如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,将下列证明EF∥CD的过程及理由填写完整.分析 先根据垂直的定义得出∠DGB=∠ACB=90°,再由平行线的判定定理得出DG∥AC,故可得出∠2=∠DCA,利用等量代换得出∠1=∠DCA,进而可得出结论.
解答 解:∵DG⊥BC,AC⊥BC(已知),
∴∠DGB=∠ACB=90°(垂直的定义),
∴DG∥AC(同位角相等,两直线平行),
∴∠2=∠DCA(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠1=∠DCA(等量代换),
∴EF∥CD(同位角相等,两直线平行).
故答案为:已知;垂直的定义;同位角相等,两直线平行;∠DCA,两直线平行,内错角相等;已知;等量代换;同位角相等,两直线平行.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
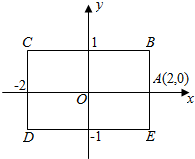 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )| A. | (-1,1) | B. | (-2,0) | C. | (-1,-1) | D. | (1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
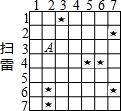 如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )
如图是小李设计的49方格扫雷游戏,“★”代表地雷(图中显示的地雷在游戏中都是隐藏的),点A可用(2,3)表示,如果小惠不想因走到地雷上而结束游戏的话,下列选项中,她应该走( )| A. | (7,2) | B. | (2,6) | C. | (7,6) | D. | (4,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com