
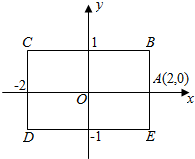
 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )| A. | (-1,1) | B. | (-2,0) | C. | (-1,-1) | D. | (1,-1) |
分析 利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
解答 解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×$\frac{1}{3}$=4,物体乙行的路程为12×$\frac{2}{3}$=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×$\frac{1}{3}$=8,物体乙行的路程为12×2×$\frac{2}{3}$=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×$\frac{1}{3}$=12,物体乙行的路程为12×3×$\frac{2}{3}$=24,在A点相遇;
…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2015÷3=671…2,
故两个物体运动后的第2014次相遇地点的是:第二次相遇地点,
即物体甲行的路程为12×2×$\frac{1}{3}$=8,物体乙行的路程为12×2×$\frac{2}{3}$=16;
此时相遇点的坐标为:(-1,-1),
故选:C.
点评 此题主要考查了点的变化规律以及行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.


科目:初中数学 来源: 题型:选择题
| A. | 黄山风景优美,是全国名山 | B. | 奥运会于2008年在北京召开 | ||
| C. | 香港是中国的一个行政区 | D. | 台湾将于2013年回归视国的怀抱 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
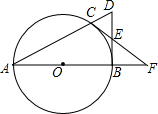 如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.
如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
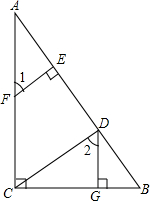 如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,将下列证明EF∥CD的过程及理由填写完整.
如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,将下列证明EF∥CD的过程及理由填写完整.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com