
【题目】如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP. 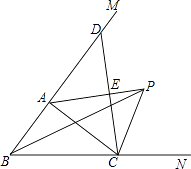
(1)求证:PA平分∠BAC的外角∠CAM;
(2)过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.
【答案】
(1)证明:
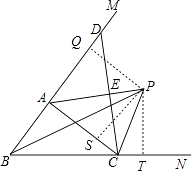
过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,如图,
∵在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,
∴PQ=PT,PS=PT,
∴PQ=PS,
∴AP平分∠DAC,
即PA平分∠BAC的外角∠CAM
(2)证明:∵PA平分∠BAC的外角∠CAM,
∴∠DAE=∠CAE,
∵CE⊥AP,
∴∠AED=∠AEC=90°,
在△AED和△AEC中
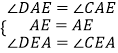
∴△AED≌△AEC,
∴CE=ED.
【解析】(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,根据角平分线性质求出PQ=PS=PT,根据角平分线性质得出即可;(2)根据ASA求出△AED≌△AEC即可.
【考点精析】掌握角平分线的性质定理是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B. 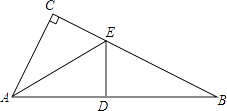
(1)求∠B的度数.
(2)如果AC=3cm,求AB的长度.
(3)猜想:ED与AB的位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,正确的是( )
A. 四边相等的四边形是正方形
B. 对角线相等的菱形是正方形
C. 正方形两条对角线相等,但不互相垂直平分
D. 矩形、菱形、正方形都具有“对角线相等”的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.如图,已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”.
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.
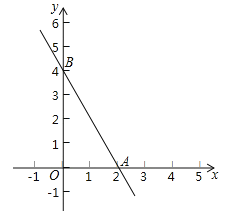
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(k+1)x2+2x﹣1=0有实数根,则k的取值范围是( )
A.k≥﹣2B.k≥﹣2且k≠﹣1C.k≥2D.k≤﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)

根据图表提供的信息,下列结论错误的是( )

A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com