
【题目】已知在平面直角坐标系中,过点![]() 向x轴作垂线,垂足为点M,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接AF,过点A作
向x轴作垂线,垂足为点M,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接AF,过点A作![]() 交y轴于点E,设点F运动的时间是t秒
交y轴于点E,设点F运动的时间是t秒![]() .
.
![]() 若点E在y轴的负半轴上
若点E在y轴的负半轴上![]() 如图所示
如图所示![]() ,求证:
,求证:![]() ;
;
![]() 如果点F运动时间是4秒.
如果点F运动时间是4秒.
![]() 求直线AE的表达式;
求直线AE的表达式;
![]() 若直线AE与x轴的交点为B,C是y轴上一点,使
若直线AE与x轴的交点为B,C是y轴上一点,使![]() ,求出C的坐标;
,求出C的坐标;
![]() 在点F运动过程中,设
在点F运动过程中,设![]() ,
,![]() ,试用含m的代数式表示n.
,试用含m的代数式表示n.
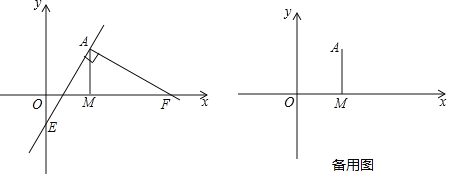
 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |

根据图表中提供的信息,解答下列问题:
(1)m= , n= , p=;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个等腰三角形ABD,AB=AD.
(1)请你用尺规作图法作出点A关于轴BD的对称点C;(不用写作法,但保留作图痕迹)
(2)连接(1)中的BC和CD,请判断四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为24的等边三角形,△CDE是等腰三角形,其中DC=DE=10,∠CDE=120°,点E在BC边上,点F是BE的中点,连接AD、DF、AF,则AF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).

(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线![]() 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
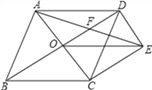
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(﹣2,0),B(0,1).
(1)点C的坐标是;
(2)将△ABC沿x轴正方向平移得到△A′B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数y= ![]() 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使得关于x的不等式组 ,有且仅有四个整数解,且使关于y的分式方程
,有且仅有四个整数解,且使关于y的分式方程![]() =1有整数解,则所有满足条件的整数a的值之和是( )
=1有整数解,则所有满足条件的整数a的值之和是( )
A. 3B. 2C. ﹣2D. ﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com