
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |

根据图表中提供的信息,解答下列问题:
(1)m= , n= , p=;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.
科目:初中数学 来源: 题型:
【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:

对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:小明在研究数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠C的数量关系.

发现:在如图中,:∠APC=∠A+∠C;如图
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)为小明的证明填上推理的依据;
(2)应用:①在如图中,∠P与∠A、∠C的数量关系为__ _;
②在如图中,若∠A=30![]() ,∠C=70
,∠C=70![]() ,则∠P的度数为__ _;
,则∠P的度数为__ _;
(3)拓展:在如图中,探究∠P与∠A,∠C的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
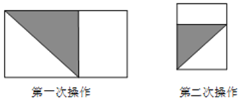
【题目】将长为1,宽为![]() 的长方形纸片
的长方形纸片![]() 如图那样折一下,剪下一个边长等于长方形的宽度的正方形
如图那样折一下,剪下一个边长等于长方形的宽度的正方形![]() 称为第一次操作
称为第一次操作![]() ;再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形
;再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形![]() 称为第二次操作
称为第二次操作![]() ;如些反复操作下去,若在第
;如些反复操作下去,若在第![]() 次操作后剩下的长方形为正方形,则操作终止.
次操作后剩下的长方形为正方形,则操作终止.
![]() 第一次操作后,剩下的长方形两边长分别为______和 ;
第一次操作后,剩下的长方形两边长分别为______和 ;![]() 用含
用含![]() 的代数式表示
的代数式表示![]()
![]() 若第二次操作后,剩下的长方形恰好是正方形,则求
若第二次操作后,剩下的长方形恰好是正方形,则求![]() 的值,写出解答过程;
的值,写出解答过程;
![]() 若第三次操作后,剩下的长方形恰好是正方形,画出图形,试求
若第三次操作后,剩下的长方形恰好是正方形,画出图形,试求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干块如左图所示的正方形或长方形纸片拼成图(1)和图(2)
(1)如图(1),若AD=7,AB=8,求![]() 与
与![]() 的值;
的值;
(2)如图(1),若长方形ABCD的面积为35,其中阴影部分的面积为20,求长方形ABCD的周长;
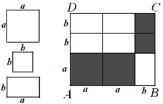
图(1)
(3)如图(2),若AD的长度为5,AB的长度为![]() .
.
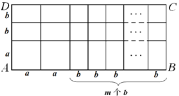
图(2)
①当![]() =________,
=________,![]() =_________时,
=_________时,![]() ,
,![]() 的值有无数组;
的值有无数组;
②当![]() ________,
________,![]() _________时,
_________时,![]() ,
,![]() 的值不存在.
的值不存在.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一矩形纸片OABC放入平面直角坐标系xoy中,使OA,OC分别落在x轴、y轴上,现将纸片OABC沿OB折叠,折叠后点A落在点A'的位置,若OA=1,OB=2,则点A'的坐标为( )
A.![]()
B.![]()
C.( ![]() )
)
D.( ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,过点![]() 向x轴作垂线,垂足为点M,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接AF,过点A作
向x轴作垂线,垂足为点M,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接AF,过点A作![]() 交y轴于点E,设点F运动的时间是t秒
交y轴于点E,设点F运动的时间是t秒![]() .
.
![]() 若点E在y轴的负半轴上
若点E在y轴的负半轴上![]() 如图所示
如图所示![]() ,求证:
,求证:![]() ;
;
![]() 如果点F运动时间是4秒.
如果点F运动时间是4秒.
![]() 求直线AE的表达式;
求直线AE的表达式;
![]() 若直线AE与x轴的交点为B,C是y轴上一点,使
若直线AE与x轴的交点为B,C是y轴上一点,使![]() ,求出C的坐标;
,求出C的坐标;
![]() 在点F运动过程中,设
在点F运动过程中,设![]() ,
,![]() ,试用含m的代数式表示n.
,试用含m的代数式表示n.
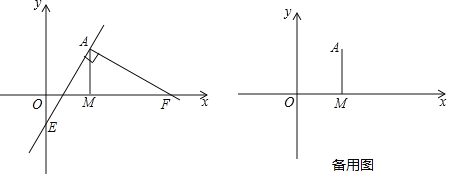
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com