
【题目】“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了![]() 条口罩生产线,每条生产线每天可生产口罩
条口罩生产线,每条生产线每天可生产口罩![]() 个.如果每增加一条生产线,每条生产线就会比原来少生产
个.如果每增加一条生产线,每条生产线就会比原来少生产![]() 个口罩.设增加
个口罩.设增加![]() 条生产线后,每条生产线每天可生产口罩
条生产线后,每条生产线每天可生产口罩![]() 个.
个.
![]() 直接写出
直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 若每天共生产口罩
若每天共生产口罩![]() 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?
个,在投入人力物力尽可能少的情况下,应该增加几条生产线?
![]() 设该厂每天可以生产的口罩
设该厂每天可以生产的口罩![]() 个,请求出
个,请求出![]() 与
与![]() 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
【答案】(1)![]() ;(2)应该增加5条生产线.(3)当增加7或8条生产线时,每天生产的口罩数量最多,为6120个.
;(2)应该增加5条生产线.(3)当增加7或8条生产线时,每天生产的口罩数量最多,为6120个.
【解析】
(1)根据“每增加一条生产线,每条生产线就会比原来少生产![]() 个口罩”即可求出y与x的函数关系式;
个口罩”即可求出y与x的函数关系式;
(2)根据题意,列出一元二次方程即可求出结论;
(3)根据题意,即可求出![]() 与
与![]() 的函数关系式,然后利用二次函数求最值即可.
的函数关系式,然后利用二次函数求最值即可.
解:(1)由题意可得:![]() ;
;
(2)由题意可得:![]()
![]()
解得:![]()
∵尽可能投入少,
∴![]() 舍去
舍去
答:应该增加5条生产线.
(3)![]() =
=![]()
∴![]()
∵![]() <0,开口向下,
<0,开口向下,
∴当x=![]() 时,w最大,
时,w最大,
又∵x为整数,所以当x=7或8时,w最大,最大值为6120.
答:当增加7或8条生产线时,每天生产的口罩数量最多,为6120个.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() ∥
∥![]() ∥
∥![]() ,一等腰Rt△ABC的三个顶点A、B、C分别在直线
,一等腰Rt△ABC的三个顶点A、B、C分别在直线![]() 、
、![]() 、
、![]() 上,∠ACB=90°,AC交
上,∠ACB=90°,AC交![]() 于点D.若
于点D.若![]() 与
与![]() 的距离为1,
的距离为1,![]() 与
与![]() 的距离为4,则
的距离为4,则![]() 的值是( )
的值是( )
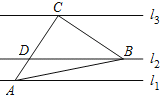
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD于点E、F.
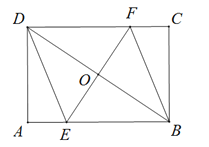
(1)求证:四边形DEBF是平行四边形;
(2)当四边形DEBF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,给出如下定义:将一个函数的图象在y轴左侧的部分沿x轴翻折,其余部分不变,两部分组成的函数图象,称为这个函数的变换图象.
(1)点A(-1,4)在函数y=x+m的变换图象上,求m的值;
(2)点B(n,2)在函数y=-x2+4x的变换图象上,求n的值;
(3)将点C(![]() ,1)向右平移5个单位长度得到点D.当线段CD与函数y= -x2+4x+t的变换图象有两个公共点,直接写出t的取值范围.
,1)向右平移5个单位长度得到点D.当线段CD与函数y= -x2+4x+t的变换图象有两个公共点,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的二次函数
的二次函数![]() 的图象开口向下,
的图象开口向下,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
下列判断,①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
④若![]() ,则
,则![]() ,正确的是________________(填写正确答案的序号) .
,正确的是________________(填写正确答案的序号) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.
类别 | 频数 | 频率 |
助人为乐美德少年 | a | 0.20 |
自强自立美德少年 | 3 | b |
孝老爱亲美德少年 | 7 | 0.35 |
诚实守信美德少年 | 6 | 0.32 |
根据以上信息,解答下列问题:
(1)统计表中的a= ,b ;
(2)统计表后两行错误的数据是 ,该数据的正确值是 ;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a,b,将其作为M点的横、纵坐标,则点M(a,b)落在以A(6,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com