【题目】正方形ABCD中，点P为直线AB上一个动点
不与点A，B重合
，连接DP，将DP绕点P旋转
得到EP，连接DE，过点E作CD的垂线，交射线DC于M，交射线AB于N．
问题出现：
当点P在线段AB上时，如图1，线段AD，AP，DM之间的数量关系为______；
题探究：
当点P在线段BA的延长线上时，如图2，线段AD，AP，DM之间的数量关系为______；
当点P在线段AB的延长线上时，如图3，请写出线段AD，AP，DM之间的数量关系并证明；
问题拓展：
在
的条件下，若
，
，则
______．
【答案】（1）
；（2）
；
，理由见解析；（3）
或
．
【解析】
根据正方形的性质和全等三角形的判定和性质得出
≌
，进而解答即可；
根据正方形的性质和全等三角形的判定和性质得出≌，进而解答即可；
根据正方形的性质和全等三角形的判定和性质得出≌，进而解答即可；
分两种情况利用勾股定理和三角函数解答即可．
解：
，理由如下：
正方形ABCD，
，
，
将DP绕点P旋转
得到EP，连接DE，过点E作CD的垂线，交射线DC于M，交射线AB于N，
，
，
，
，
，
，
在
与
中，
，
≌
，
，
，
；
，理由如下：
正方形ABCD，
，，
将DP绕点P旋转得到EP，连接DE，过点E作CD的垂线，交射线DC于M，交射线AB于N，
，，，
，，
，
在与中，
，
≌，
，，
；
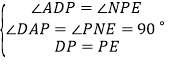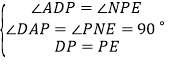，理由如下：
，
，
，
又
，
，
≌
，
，
；
有两种情况，如图2，
，如图3，
；
如图2：
，
，
在
中
，
，
；
如图3：，
，
在中，，
，
．
故答案为；；
；或．
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案科目：初中数学 来源： 题型：
【题目】如图，在一棵树CD的10m高处的B点有两只猴子，它们都要到A处池塘边喝水，其中一只猴子沿树爬下走到离树20m处的池塘A处，另一只猴子爬到树顶D后直线跃入池塘的A处．如果两只猴子所经过的路程相等，试问这棵树多高？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校在“清明节”前组织七年级全体学生进行了一次“缅怀先烈，牢记历史”知识竞赛，赛后随机抽取了部分学生成绩进行统计，制作如下频数分布表和频数分布直方图，请根据图中提供的信息，解答下列问题：
分数段 | 频数 | 频率 |
| 4 |
|
| 8 | b |
| a |
|
| 10 |
|
| 6 |
|
表中
______，
______，并补全直方图；
若用扇形统计图描述次成绩统计图分别情况，则分数段
对应扇形的圆心角度数是______；
若该校七年级共900名学生，请估计该年级分数在
的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)如图1，将长方形ABCD折叠，使BC落在对角线BD上，折痕为BE，点C落在点C′处，若∠ADB=48°，则∠DBE的度数为_______.
(2)小明手中有一张长方形纸片ABCD，AB=12，AD=27.
（画一画）
如图2，点E在这张长方形纸片的边AD上，将纸片折叠，使AB落在CE所在直线上，折痕设为MN(点M，N分别在边AD，BC上)，利用直尺和圆规画出折痕MN(不写作法，保留作图痕迹，).
（算一算）
如图3：点F在这张长方形纸片的边BC上，将纸片折叠，使FB落在线段FD上，折痕为GF，点A、B分别落在点E、H处，若△DCF的周长等于48，求DH和AG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，交AB于点E．
（1）求证：△ABD是等腰三角形；
（2）若∠A=40°，求∠DBC的度数；
（3）若AE=6，△CBD的周长为20，求△ABC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．
（1）求证：DE=DF；
（2）若∠A=60°，BE=1，求△ABC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A(－1，0)，B(0，2)，点C在x轴上，且∠ABC＝90°.
(1)求点C的坐标；
(2)求经过A，B，C三点的抛物线的表达式；
(3)在(2)中的抛物线上是否存在点P，使∠PAC＝∠BCO？若存在，求出点P的坐标；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
