
【题目】“ 六一”儿童节前夕,某县教育局准备给留守儿童赠送一批学习用品,先对某小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.
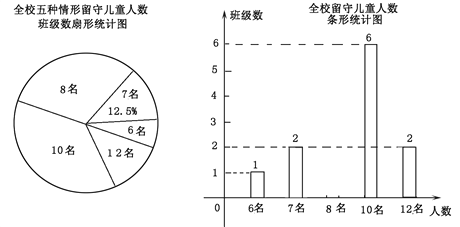
请根据上述统计图,解答下列问题:
(1)该校有_______个班级;各班留守儿童人数的中位数是_______;并补全条形统计图;
(2)若该镇所有小学共有65 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
【答案】 16 9名
【解析】分析:(1)根据有7名留守儿童班级有2个,所占的百分比是12.5%,即可求得班级的总个数,根据中位数的概念求出中位数,求出留守儿童人为8名的班级数,补全条形统计图;
(2)求出每班的留守儿童的平均数,利用班级数65乘以平均数即可.
详解:(1)该校的班级数是:2÷12.5%=16(个),
中位数是![]() (名),
(名),
留守儿童人数为8名的班级数为:161262=5,
补全条形统计图如图:
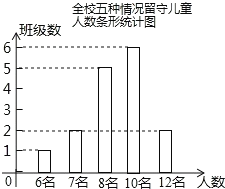
故答案为:16;9名;
(2)每班的留守儿童的平均数是:![]() (1×6+2×7+5×8+6×10+12×2)=9(人),
(1×6+2×7+5×8+6×10+12×2)=9(人),
则该镇小学生中,共有留守儿童65×9=585(人).
答:该镇小学生中共有留守儿童585人


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即![]() m/s),交通管理部门在离该公路100m处设置了一速度检测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上.
m/s),交通管理部门在离该公路100m处设置了一速度检测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)在图中直接标出表示60°和45°的角;
(2)写出点B、点C坐标;
(3)一辆汽车从点B匀速行驶到点C所用时间为15s.请你通过计算,判断该汽车在这段限速路上是否超速?(本小问中![]() 取1.7)
取1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:


根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
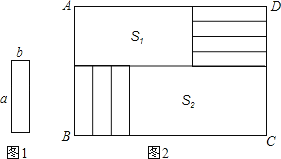
【题目】将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
⑴当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S1﹣S2的值为 .
⑵当AD=40时,请用含a、b的式子表示S1﹣S2的值;
⑶若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S1﹣S2的值总保持不变,则a、b满足的什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() ,点
,点![]() .
.
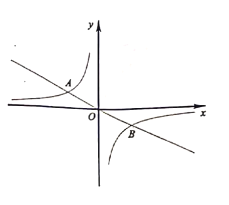
(1)求反比例函数![]() 的表达式;
的表达式;
(2)根据图象直接写出不等式![]() 的解集 .
的解集 .
(3)将直线![]() 沿
沿![]() 轴向下平移后,分别与
轴向下平移后,分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() ,点
,点![]() ,当四边形
,当四边形![]() 为平行四边形时,求直线
为平行四边形时,求直线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).
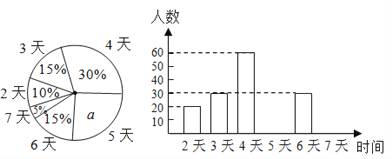
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中a的值,并求出该校初一学生总数;
(2)分别求出活动时间为5天、7天的学生人数,并补全频数分布直方图;
(3)求出扇形统计图中“活动时间为4天”的扇形所对圆心角的度数;
(4)在这次抽样调查中,众数和中位数分别是多少?
(5)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为
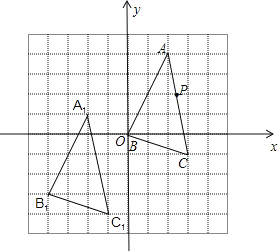
A.(1.4,-1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com