
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.AO交⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,
,
(1)求 ![]() 的值.
的值.
(2)设⊙O的半径为3,求AB的长.
【答案】
(1)解:如图,过点O作OF⊥AB于点F,

∵AO平分∠CAB,
OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线;
连接CE,
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴ ![]() =
= ![]() ,
,
∵tan∠D= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
(2)解:

由(1)可知: ![]() =
= ![]() ,
,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴ ![]() =
= ![]() ,
,
∴AC2=AEAD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2,AC=4,
由(1)可知:AC=AF=4,
∠OFB=∠ACB=90°,
∵∠B=∠B,
∴△OFB∽△ACB,
∴ ![]() =
= ![]() ,
,
设BF=a,
∴BC= ![]() ,
,
∴BO=BC﹣OC= ![]() ﹣3,
﹣3,
在Rt△BOF中,
BO2=OF2+BF2,
∴( ![]() ﹣3)2=32+a2,
﹣3)2=32+a2,
∴解得:a= ![]() 或a=0(不合题意,舍去),
或a=0(不合题意,舍去),
∴AB=AF+BF= ![]() .
.
【解析】(1)可把∠D放在直角三角形中,须连接CE,OF,证出△ACE∽△ADC,利用对应边成比例转化![]() ;(2)利用(1)的结果求出AE、AC,证出△OFB∽△ACB,列出比例式,利用勾股定理建立方程,求出AB.
;(2)利用(1)的结果求出AE、AC,证出△OFB∽△ACB,列出比例式,利用勾股定理建立方程,求出AB.
【考点精析】掌握圆周角定理和相似三角形的判定与性质是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】在网络时代里,每年网络上都会出现很多红极一时的网络流行语,为了解同学们对网络流行语的使用情况,某数学兴趣小组选取了其中的 A:“蓝瘦香菇”,B:“洪荒之力”,C:“老司机”,D:“套路”四个网络流行语在全校3000名学生中进行了抽样调查,要求每位被调查学生只能从中选择一个自己用得最多的网络流行语.根据调查结果,该小组绘制了如下两幅不完整的统计图,根据图中提供的信息,请补全条形统计图并估计该校学生用得最多的网络流行语.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,则∠BDC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠ABC的平分线BE交CD于点E,∠ADC的平分线DF交AB于点F.
(1)若AD=4,AB=6,求BF的长.
(2)求证:四边形DEBF是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小彬和爸爸一起去车站接从外地学习回来的妈妈,在去的过程中,小彬坐在汽车上看着时速表,用所学知识绘制了一张反映小车速度与时间的关系图,请你根据图象回答以下问题:

(1)在上述过程中,自变量是什么?因变量是什么?
(2)小车共行驶了多少时间?最高时速是多少?
(3)汽车在哪段时间保持匀速运动?速度是多少?
(4)汽车在哪段时间内速度在增加?哪段时间内速度在减少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,线段
,线段![]() ,线段
,线段![]() ,且
,且![]() ,
,![]() 与
与![]() 的交点记为
的交点记为![]() ,连接
,连接![]() .
.
(1)求![]() 的面积.
的面积.
(2)如图2,在线段![]() 上有两个动点
上有两个动点![]() 、
、![]() (
(![]() 在
在![]() 点上方),且
点上方),且![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 的值最小时,求出此时
的值最小时,求出此时![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,在![]() 轴上找一点
轴上找一点![]() ,
,![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 取得最小值,请求出
取得最小值,请求出![]() 的最小值.
的最小值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的个数是( )个
,其中正确的个数是( )个
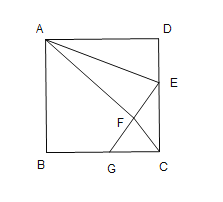
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com