
【题目】如图,在平面直角坐标系中,平行四边形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,线段
,线段![]() ,线段
,线段![]() ,且
,且![]() ,
,![]() 与
与![]() 的交点记为
的交点记为![]() ,连接
,连接![]() .
.
(1)求![]() 的面积.
的面积.
(2)如图2,在线段![]() 上有两个动点
上有两个动点![]() 、
、![]() (
(![]() 在
在![]() 点上方),且
点上方),且![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 的值最小时,求出此时
的值最小时,求出此时![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,在![]() 轴上找一点
轴上找一点![]() ,
,![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 取得最小值,请求出
取得最小值,请求出![]() 的最小值.
的最小值.


【答案】(1)![]() ;(2)
;(2)![]() ,(3)
,(3)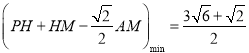 ;
;
【解析】
(1)过点D作DP⊥AB于点P,则利用直角三角形的性质和勾股定理求出DP的长度,即可得到答案;
(2)根据题意,作点F关于BE的对称点H,过点H作HI∥BE,取HI=KG=![]() ,过点I作y轴的平行线,交AB于点J,交BE于点K,交CD于点P,此时
,过点I作y轴的平行线,交AB于点J,交BE于点K,交CD于点P,此时![]() 得到最小值,由轴对称的性质,勾股定理,30度直角三角形的性质,求出BG的长度,然后求出BJ的长度,即可得到点P的坐标;
得到最小值,由轴对称的性质,勾股定理,30度直角三角形的性质,求出BG的长度,然后求出BJ的长度,即可得到点P的坐标;
(3)如图,作点P关于y轴的对称点![]() ,作
,作![]() ,交x轴于点M,交y轴于点H,则此时
,交x轴于点M,交y轴于点H,则此时![]() 最小;由等腰直角三角形的性质和勾股定理求出
最小;由等腰直角三角形的性质和勾股定理求出![]() 的长度,然后求出AM的长度,即可求出最小值.
的长度,然后求出AM的长度,即可求出最小值.
解:(1)如图,过点D作DP⊥AB于点P,
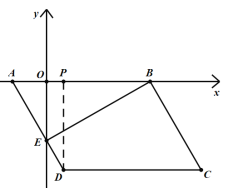
∵![]() ,
,
∴![]() ,
,
在Rt△ADP中,AD=6,
∴AP=3,
由勾股定理,得
![]() ,
,
∴![]() ;
;
(2)如图,作点F关于BE的对称点H,过点H作HI∥BE,取HI=KG=![]() ,过点I作y轴的平行线,交AB于点J,交BE于点K,交CD于点P,此时
,过点I作y轴的平行线,交AB于点J,交BE于点K,交CD于点P,此时![]() 得到最小值;
得到最小值;
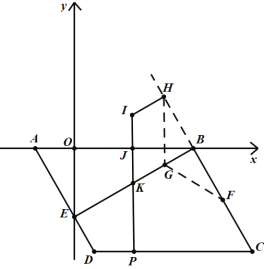
则四边形KGHI是平行四边形,
∴HG=IK=FG,HI=KG=![]() ,
,
在Rt△AOE中,∠OAE=60°,OA=2,
∴∠AEO=30°,
∴AE=2OA=4,
∴OE=![]() ,
,
在Rt△OBE中,OB=6,
∴![]() ,
,
∵![]() ,
,
∴△ABE是直角三角形,即AE⊥BE,
∴∠ABE=30°,∠FBG=90°,
∴∠BGH=∠BGF=60°,
∴∠BFG=30°,
∴![]() ,
,
∵点F为BC中点,
∴BF=3,
由勾股定理,得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△BJK中,∠ABE=30°,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴点P的坐标为:(3,![]() );
);
(3)如图,作点P关于y轴的对称点![]() ,作
,作![]() ,交x轴于点M,交y轴于点H,则此时
,交x轴于点M,交y轴于点H,则此时![]() 最小;
最小;
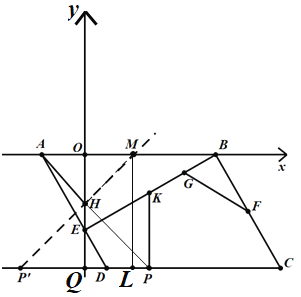
由轴对称的性质,得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ;
;
∵AB∥CD,
∴四边形OMLQ是矩形,
∴OM=QL=![]() ,
,
∴AM=![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为18dm2和32dm2的正方形木板.

(1)求剩余木料的面积.
(2)如果木工想从剩余的木料中截出长为1.5dm,宽为ldm的长方形木条,最多能截出 块这样的木条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.AO交⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,
,
(1)求 ![]() 的值.
的值.
(2)设⊙O的半径为3,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“绿满重庆”行动中,江北区种植了大量的小叶榕和银杏树,根据林业专家的分析,树叶在进行光合作用后产生的分泌物能在空气中吸附悬浮颗粒,这样就达到了滞尘净化空气的作用.
(1)若某小区今年要种植银杏树和小叶榕共450株,且银杏树的数量不超过小叶榕数量的2倍,求今年该小区小叶榕至少种植多少株?
(2)已知每一片银杏树叶一年平均滞尘量为![]() ,一株银杏树去年有3500片树叶,冬季树叶全部掉落后,今年新长出了树叶,且这株银杏今年的滞尘量是去年滞尘量的1.1倍还多
,一株银杏树去年有3500片树叶,冬季树叶全部掉落后,今年新长出了树叶,且这株银杏今年的滞尘量是去年滞尘量的1.1倍还多![]() .已知每片小叶榕树叶的滞尘量比银杏树叶多
.已知每片小叶榕树叶的滞尘量比银杏树叶多![]() ,一株小叶榕今年的树叶总量比今年的这株银杏要少
,一株小叶榕今年的树叶总量比今年的这株银杏要少![]() ,明年这株小叶榕树叶将在今年的基础上掉落
,明年这株小叶榕树叶将在今年的基础上掉落![]() ,但又会新长出1000片树叶,若今明两年这株小叶榕共滞尘量为
,但又会新长出1000片树叶,若今明两年这株小叶榕共滞尘量为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ![]() ,点A,B,E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
,点A,B,E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )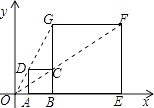
A.(2,2)
B.(3,1)
C.(3,2)
D.(4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2![]() ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF

(1)如图1,求证:AE=CF;
(2)如图2,若A,E,O三点共线,求点F到直线BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一枚质地均匀的正四面体骰子,它的四个面上分别标有数字0,1,2,3,如图2,正方形ABCD的四个顶点处均有一个圈.课间,李丽和王萍利用它们玩跳圈游戏,玩法如下:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形ABCD的边顺时针分钟连续跳几个边长.
例如:若从圈A起跳,第一掷得的数字为2,便沿正方形的边顺时针连续跳2个边长,落到圈C,第二次掷得的数字为3,便从圈C开始,沿正方形的边顺时针连续跳3个边长,落到圈B,….
设她们从圈A起跳.
(1)若李丽随机掷这枚骰子一次,求她跳回圈A的概率;
(2)若王萍随机掷这枚骰子两次,请用列表法或画树状图求她最后跳回圈A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿矩形的边由![]() 运动,设点P运动的路程为x,
运动,设点P运动的路程为x,![]() 的面积为y,把y看作x的函数,函数的图像如图2所示,则
的面积为y,把y看作x的函数,函数的图像如图2所示,则![]() 的面积为( )
的面积为( )

A. 10 B. 16 C. 18 D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com