
【题目】如图1是一枚质地均匀的正四面体骰子,它的四个面上分别标有数字0,1,2,3,如图2,正方形ABCD的四个顶点处均有一个圈.课间,李丽和王萍利用它们玩跳圈游戏,玩法如下:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形ABCD的边顺时针分钟连续跳几个边长.
例如:若从圈A起跳,第一掷得的数字为2,便沿正方形的边顺时针连续跳2个边长,落到圈C,第二次掷得的数字为3,便从圈C开始,沿正方形的边顺时针连续跳3个边长,落到圈B,….
设她们从圈A起跳.
(1)若李丽随机掷这枚骰子一次,求她跳回圈A的概率;
(2)若王萍随机掷这枚骰子两次,请用列表法或画树状图求她最后跳回圈A的概率.
【答案】
(1)解:∵共有4种等可能的结果,落回到圈A的只有1种情况,
∴落回到圈A的概率P1= ![]()
(2)解:列表得:
1 | 2 | 3 | 0 | |
1 | (1,1) | (2,1) | (3,1) | (0,1) |
2 | (1,2) | (2,2) | (3,2) | (0,2) |
3 | (1,3) | (2,3) | (3,3) | (0,3) |
0 | (1,0) | (2,0) | (3,0) | (0,0) |
∵共有16种等可能的结果,最后落回到圈A的有4种情况,
∴最后落回到圈A的概率P= ![]() =
= ![]()
【解析】(1)利用概率公式,关注的结果除以机会均等的结果即可求出;(2)事件分为两个步骤,可列表,机会均等的情况为16种,跳回A圈的有4种,可得概率为![]() .
.
【考点精析】通过灵活运用列表法与树状图法和概率公式,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n即可以解答此题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,则∠BDC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() ,线段
,线段![]() ,线段
,线段![]() ,且
,且![]() ,
,![]() 与
与![]() 的交点记为
的交点记为![]() ,连接
,连接![]() .
.
(1)求![]() 的面积.
的面积.
(2)如图2,在线段![]() 上有两个动点
上有两个动点![]() 、
、![]() (
(![]() 在
在![]() 点上方),且
点上方),且![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 的值最小时,求出此时
的值最小时,求出此时![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,在![]() 轴上找一点
轴上找一点![]() ,
,![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 取得最小值,请求出
取得最小值,请求出![]() 的最小值.
的最小值.


查看答案和解析>>
科目:初中数学 来源: 题型:
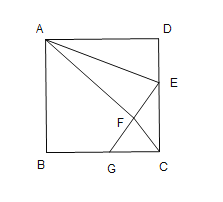
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的个数是( )个
,其中正确的个数是( )个
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.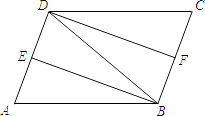
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=6cm,动点P以2cm/s的速度从A﹣B﹣A在线段AB上运动,到达点A后,停止运动;动点Q以1cm/s的速度从B﹣A在线段AB上运动,到达点A后,停止运动.若动点P,Q同时出发,设点Q的运动时间是t(单位:s)时,两个动点之间的距离为S(单位:cm),则能表示S与t的函数关系的是( )
![]()
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.

小题1:如图1,可以求出阴影部分的面积是_______ (写成两数平方差的形式);
小题2:如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______,长是______,面积是_________ (写成多项式乘法的形式).
小题3:比较图 1,图2的阴影部分面积,可以得到乘法公式________ (用式子表达).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com